Перечислите этапы построения сценария процесса моделей

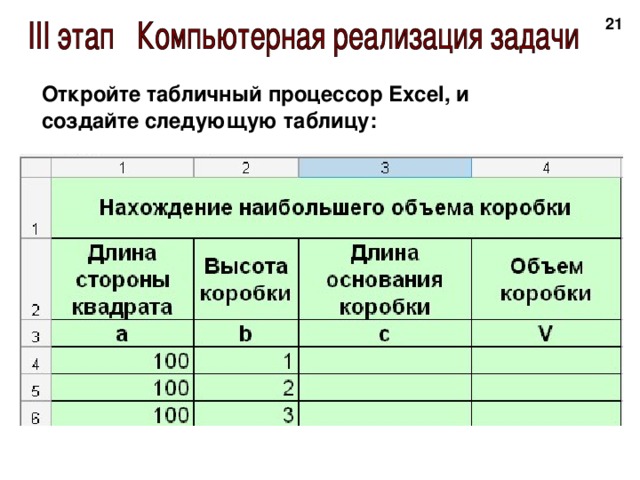
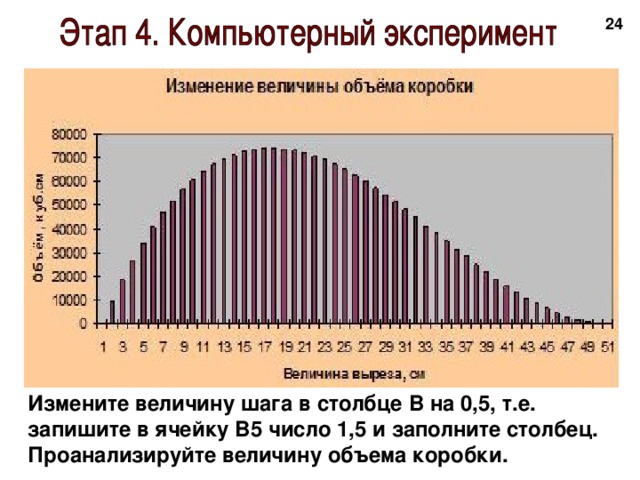
Информационное моделирование – это творческий процесс. Не существует универсального рецепта построения моделей, пригодного на все случаи жизни, но можно выделить основные этапы и закономерности, характерные для создания самых разных моделей.

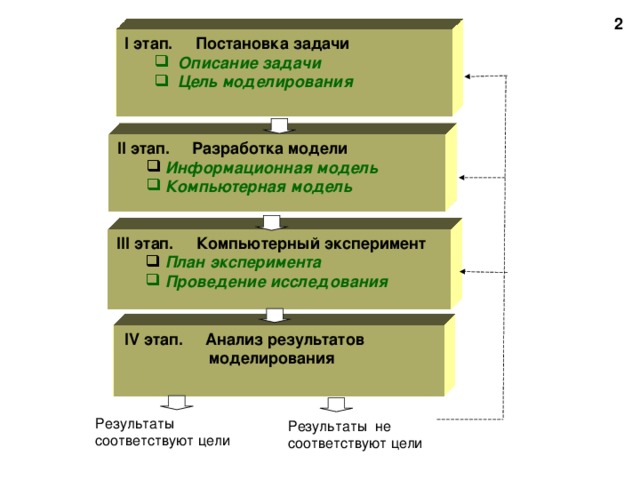
Первый этап – постановка задачи. Прежде всего следует уяснить цель моделирования. Исходя из цели моделирования, определяется вид и форма представления информационной модели, а также степень детализации и формализации модели. В соответствии с целью моделирования заранее определяются границы применимости создаваемой модели. На этом этапе также необходимо выбрать инструментарий, который будет использоваться при моделировании (например, компьютерную программу).

Второй этап – собственно моделирование, построение модели. На этом этапе важно правильно выявить составляющие систему объекты, их свойства и взаимоотношения и представить всю эту информацию в уже выбранной форме. Создаваемую модель необходимо периодически подвергать критическому анализу, чтобы своевременно выявлять избыточность, противоречивость и несоответствие целям моделирования.

Третий этап – оценка качества модели, заключающаяся в проверке соответствия модели целям моделирования. Такая проверка может производиться путем логических рассуждений, а также экспериментов, в том числе и компьютерных. При этом могут быть уточнены границы применимости модели. В случае выявления несоответствия модели целям моделирования она подлежит частичной или полной переделке.

Четвертый этап – эксплуатация модели, ее применение для решения практических задач в соответствии с целями моделирования.

Пятый этап – анализ полученных результатов и корректировка исследуемой модели.

Источник

Упрощенно
процесс моделирования содержит
следующие этапы:

1.
Постановка цели моделирования.

2.
Разработка концептуальной модели.

3.
Подготовка исходных данных.

4.
Разработка математической модели.

5.
Выбор метода моделирования.

6.
Выбор средств моделирования.

7.
Разработка программной модели.

8.
Проверка адекватности (тождественности)
и корректировка модели.

9.
Планирование машинных экспериментов.

10.
Моделирование на ЭВМ.

11.
Анализ результатов.

При
моделировании различных систем
трудоемкость одних и тех же этапов может
быть различной. Например, метод
моделирования или средство моделирования
могут быть определены заранее. Если
математическая модель оказывается
очень простой, то не требуется машинное
моделирование или разработка программной
модели может исключать создание
математической модели.

Особо
важным является первый этап, поскольку
все последующие этапы моделирования
должны ориентироваться на конкретную
цель. На этом же этапе рассматривается
вопрос о единицах измерения результатов
моделирования – относительных (лучше
– хуже, больше – меньше), дающих
качественную оценку, и абсолютных. В
последнем случае решается вопрос о
точности измерения.

Проверка
адекватности модели, хотя и выделена
отдельным этапом, должна проводиться
на всех этапах, начиная с разработки
концептуальной модели и кончая анализом
результатов моделирования.

На
этапе разработки математической модели
создается полностью формализованное
описание функционирования системы на
базе одного из разделов математики, но
не для всех сложных систем условия их
взаимодействия с внешней средой и цели
моделирования могут быть описаны с
помощью математического аппарата. Для
таких систем необходимо разрабатывать
однозначные зависимости характеристик
от параметров и внешних воздействий
для каждого элемента системы.

Анализ
результатов моделирования должен
выполняться обязательно, чтобы проверить
их достоверность и выработать рекомендации
о способах повышения качества исследуемой
системы.

1.3.1. Постановка цели моделирования

Перед
разработкой модели необходимо
сформулировать цели моделирования, т.
к. для одной и той же системы S₀можно создать множество
моделей S_mв
зависимости от решаемой задачи, могут
существенно отличаться друг от друга.

Как
правило, при проектировании или
модернизации любой системы возникает
задача оценки ее эффективности, или
выбор наиболее эффективного варианта.
Решение этих задач и является главными
целями моделирования.

В
зависимости от типа системы и вида задач
конкретизируется понятие эффективности
системы.

Эффективность
может характеризоваться превышением
стоимости эксплуатации над затратами
на создание системы. Такой подход
используется для реальных работающих
систем, но для проектируемых систем
подсчет затрат на эксплуатацию сложен.

Кроме
того, поскольку каждая система может
быть элементом системы более высокого
уровня, а та, в свою очередь, – элементом
системы еще более высокого уровня, и
все эти системы взаимосвязаны, определить
эффективность системы по стоимости
практически оказывается невозможным.

Например,
ВС, входящая в состав ИВЦ, используется
в системе обучения студентов, в системе
управления набором и обучением студентов,
в системе научных и технических
разработок, информационного обеспечения
и т. д. Одновременно эта ВС является
элементом систем энергоснабжения,
технического обслуживания, материального
снабжения и т. д. Очевидно, оценить в
единых единицах общую эффективность
данной системы практически невозможно.

В
этом случае используется понятие
технико-экономической эффективности,
которая учитывает затраты и измеряемые
характеристики системы:

_{E=E(Y0), (1.3)}

где
множество характеристик Y₀– это производительность,
надежность, стоимость, масса, габаритные
размеры и т. д.; Е – показатель эффективности.

Если
известны функции (1.1) и (1.3), то показатель
эффективности можно вычислить по
множеству параметров системы S₀
при определенных внешних воздействиях
X₀.

Если
известны обратные зависимости, т.е. y_0k
= F(E), то задача моделирования становится
тривиальной, т.к. параметры системы
оказывается возможным вычислить по
заданному показателю эффективности.
Если эффективность системы оценивается
по одному частному показателю качества
y_opt,
а по остальным характеристикам накладывают
ограничения на допустимые изменения,
то

_E=yopt;

_{yimin<=yi <=yimax,

i=1,…,n.}

где
y_imin,y_imax
– нижний и верхний пределы i-го показателя
качества; а n – число учитываемых
характеристик системы, и оценка
эффективности называется однокритериальной.
Недостаток однокритериальной оценки:
при нескольких вариантах системы с
одинаковыми значениями y_opt
при существенно различающихся других
показателях качества невозможно
определить наилучший вариант системы.

При
многокритериальной оценке функция
(1.3) представляется в форме интегрального
(обобщенного) критерия, который достаточно
просто связывает показатель эффективности
со всеми учитываемыми характеристиками
системы.

Н
аиболее
распространен нормированный аддитивный
критерий

г
де
функции (y_i)
подбираются так, чтобы обеспечивалось
условие (y_i){0,1},
а весовые коэффициенты b_i,
согласующие шкалы измерений различных
характеристик, должны удовлетворять
условию

Если
0
y_i
y_imax
и (y_i)
= y_i/y_imax,
нормированный аддитивный критерий
становится линейным. Сложность
многокритериальной оценки – определение
весовых коэффициентов b_i.

Таким
образом, постановка цели моделирования
заключается, прежде всего, в выборе
критерия эффективности E исследуемой
системы, т.е. задание множества
характеристик Y_0k,
их весовых коэффициентов и допустимых
пределов изменения.

Кроме
того, из множества характеристик Y_0k
следует исключить те, которые могут
быть определены без моделирования,
конкретизировать внешние воздействия
X_0nХ₀,
при наличии которых функционирует
система и определить интервал времени
Т₀работы
системы. Множество внешних воздействий
должно включать как полезные воздействия,
способствующие функционированию
системы, так и возмущающие, препятствующие
работе системы. При этом не все возмущающие
воздействия целесообразно учитывать
при моделировании, т.е. допускается
некоторая идеализация работы системы.
Временной интервал Т₀
должен отражать период активного
функционирования системы, если за это
время значения внешних воздействий
изменяются, то они должны быть заданы
как функции времени Х_on(t).
Временной интервал T_о
может быть как непрерывным, так и
дискретным.

Целью
моделирования является не только оценка
эффективности, но и оптимизация системы,
в этом случае необходимо выделить те
параметры, которые можно изменить –
S_jS₀и выбрать критерий
оптимизации (см. разд. 3). Также целью
моделирования может быть выявление
функциональных зависимостей характеристик
системы от параметров (1.2).

При
определении целей моделирования также
задается точность получения результатов
моделирования.

И,
наконец, на первом этапе необходимо
решить вопрос о целесообразности
проведения моделирования, т.к. затраты
на моделирование возрастают пропорционально
сложности системы и точности получаемых
результатов. Если моделирование
проводится с целью обоснования
работоспособности системы, то экономический
эффект от эксплуатации данных систем
должен превосходить затраты на
моделирование. Если целью моделирования
является оптимизация системы, то затраты
на моделирование должны окупаться за
счет разницы между наилучшим и наихудшим
вариантами системы.

1.3.2. Разработка концептуальной модели

В
процессе разработки модель создается
в трех видах: концептуальная, математическая
и программная.

Концептуальная
(содержательная) модель – это абстрактная
модель, определяющая состав и структуру
системы, свойства элементов S₀и связи, присущие
исследуемой модели.

Концептуальная
модель – словесное описание природы
и параметров элементарных явлений
исследуемой системы, видов и способов
взаимодействия между ними, значений
каждого элементарного явления в общем
процессе функционирования системы.

Основой
для создания концептуальной модели
являются цели моделирования.

Основной
проблемой при создании модели является
нахождение компромисса между простотой
модели и ее адекватностью с исследуемой
системой. Очевидно, что процесс создания
концептуальной модели не может быть
полностью формализован.

При
создании концептуальной модели необходимо
выбрать уровень детализации модели.
Это можно сделать путем построения
иерархической последовательности
моделей. Моделируемая система
представляется семейством моделей,
каждая из которых отображает ее поведение
на различных уровнях детализации. На
каждом уровне исследуют характерные
особенности системы, с помощью которых
описывают поведение системы. Уровни
детализации иногда называют стратами,
а процесс выделения уровней –
стратификацией.

Выбор
уровня моделирования зависит от целей
моделирования. Для одной и той же системы
можно выделять различные уровни
детализации.

Обычно
в модель включаются элементы одного
уровня детализации, но можно построить
модель и из разных уровней, если на более
общем уровне свойства отдельных элементов
мало известны или трудно составить их
описание.

Правило
построения стратифицированной
концептуальной модели:

в
модель входят те параметры системы
S_ok,
которые обеспечивают определение
характеристик Y_ok
при некоторых внешних воздействиях X_on
на заданном временном интервале Т
функционирования системы, и, в первую
очередь, параметры, допускающие
варьирования в процессе моделирования
– S_oj;
остальные параметры могут быть исключены
из модели.

Правило
расчленения системы на элементы:

каждый
элемент обеспечивает выполнение
элементарных операций в системе, поэтому
в модели должны присутствовать параметры,
реализующие выполнение всех технических
процессов (преобразование информации,
энергии, вещества), а также элементы,
управляющие ресурсами и процессами и
обеспечивающие хранение информации.

Детализация
системы должна производиться до такого
уровня, чтобы для каждого элемента можно
было получить зависимости выходных
характеристик от входных воздействий.

После
детализации проводится локализация
концептуальной модели, которая
осуществляется путем представления
внешней среды в виде генераторов внешних
воздействий, включаемых в состав модели
в качестве элементов. Генераторы внешних
воздействий разделяются на генераторы
рабочей нагрузки, поставляющие на вход
системы основные исходные объекты —
энергию, данные для ВС; генераторы
управляющих и возмущающих воздействий.
Генераторы возмущающих воздействий
нарушают процесс функционирования
системы.

Приемники
выходных воздействий обычно в модель
не включают, т.к. считается, что результаты
функционирования системы внешняя среда
принимает полностью и без задержек.

Завершается
построение концептуальной модели
указанием связей между элементами,
которые подразделяются на вещественные
и информационные. Вещественные связи
отражают возможные перемещения
предмета преобразования от одного
элемента к другому, а информационные
связи обеспечивают передачу между
элементами управляющих воздействий.
Эти связи не обязательно должны
быть представлены материальным
каналом связи; более того, в простых
системах, элементы которых имеют по
одной выходной вещественной связи,
информационные связи могут вообще
отсутствовать. Управление процессом
функционирования в таких системах
определяется структурой системы.
Примерами подобных систем могут
служить логические элементы.

В
более сложных системах, включающих
многофункциональные элементы или
элементы, имеющие более чем по
одной выходной вещественной связи,
имеются управляющие средства
(решающие элементы) и соответствующие
информационные связи. Это системы,
которые функционируют в соответствии
с программным или алгоритмическим
принципом управления.

В
концептуальной модели также должны
быть конкретизированы все решающие
правила или алгоритмы управления
рабочей нагрузкой, элементами и
процессами.

Модель,
составленная в соответствии с
изложенными правилами, соответствует
системе в статике, т.е. описывает её
состав и структуру. Для представления
динамической системы модель следует
дополнить описанием работы системы.

Динамику
функционирования системы отражают
совокупность алгоритмов управления
A₀,
параметров входных воздействий X₀
и элементов S₀,
т.е. множество характеристик динамической
системы определяется так:

Y = Ф(X,S,A,T). (1.4)

Для
систем со структурным принципом
управления динамика функционирования
представляется в виде последовательной
смены состояний Z(t₀),
Z(t₁),
… , Z(T). Если известно начальное
состояние системы Z₀= Z(t₀),
то можно определить ее состояние в
любой момент tT,
при известной зависимости Z(t) =
H(X,Z₀,Z,t).

Выходные
характеристики в этом случае
определяются так

Y = G(Z,T),

Z(t)
= H(X, Z₀,
Z, t), (1.5)

где
Z(t) — текущее состояние системы, G,Ф
–операторы выходов, H – оператор
переходов.

Разработанная
концептуальная модель проверяется
на адекватность исследуемому объекту

1.3.3. Подготовка исходных данных

В
процессе создания концептуальной
модели выявляются качественные и
количественные параметры системы S₀
и внешних воздействий X₀,
и определяются их конкретные значения.

Подготовка
исходных данных может проходить
параллельно с разработкой концептуальной
модели.

Подбор
исходных данных связан с определенными
трудностями:

во-первых,
значения параметров могут быть не
только детерминированными, но и
стохастическими;

во-вторых,
не все параметры оказываются
стационарными, особенно для внешних
воздействий;

в-третьих,
обычно моделируется проектируемая
система, которая должна функционировать
в новых условиях.

В
целях упрощения модели случайные
параметры представляются детерминированными
средними значениями в том случае,
если случайная величина имеет небольшой
разброс. Например, производительность
процессора может быть задана
определенным количеством операций,
выполняемых в единицу времени. Это
количество детерминировано для
определенных операций, выполняемых
процессором.

При
создании модели может иметь место
и замена детерминированных параметров
случайной величиной, при интеграции
элементов системы или внешних
воздействий с целью сокращения
размерности модели. Например, для
моделирования многократного выполнения
программы можно вместо задания
совокупности параметров задать
случайную величину с определенным
законом распределения.

Для
случайных параметров собирается
статистика, выявляется возможность
представления параметра некоторым
теоретическим законом распределения.

Особую
сложность представляет сбор данных
по нестационарным случайным параметрам,
какими являются параметры внешних
воздействий. Пренебрежение
нестационарностью может привести к
существенным нарушениям адекватности
модели.

В
процессе подготовки исходных данных
необходимо проводить аппроксимацию
функций, связывающих параметры входных
воздействий и выходные характеристики
в том случае, если указанная функциональная
связь не очевидна, а может быть
получена в ходе эксперимента.

Для
параметров, отражающих новые элементы
или условия функционирования, и для
которых невозможен сбор данных,
выдвигается гипотеза относительно
их возможных значений. При этом
используется информация об аналогах
или прототипах системы.

Заканчивается
этап сбора и обработки данных их
классификацией на:

внешние и
внутренние;
постоянные
и переменные;
непрерывные
и дискретные;
линейные и
нелинейные;
стационарные
и нестационарные;
детерминированные
и стохастические, и т.п.

Для
переменных, варьируемых в ходе
моделирования, определяются границы
изменения, а для дискретных — возможные
значения.

1.3.4. Разработка математической модели

Концептуальная
модель и количественные исходные
данные служат основой для разработки
математической модели системы.

Создание
математической модели преследует две
цели:

дать
формализованное описание структуры
и процесса функционирования системы
для однозначности их понимания;

представить
процесс функционирования в виде,
допускающем аналитическое исследование
системы.

Вследствие
разнообразия классов систем разработать
единую методику создания математической
модели невозможно. Для некоторых систем
математические модели уже известны.
Например, для динамических систем без
предыстории с алгоритмическим принципом
управления математическая модель –
это зависимость вида (1.4), а для систем
со структурным принципом управлением
математическая модель обычно представляется
в виде (1.5).

Для
других классов систем разработаны
специальные формализованные схемы и
математические методы, позволяющие
описывать функционирование системы и
выполнять исследования.

1)
Агрегативные системы (AC). Это одна из
наиболее общих формализованных схем.
Метод АС позволяет представлять
функционирование непрерывных и
дискретных, детерминированных и
стохастических систем. В наибольшей
степени этот метод пригоден для описания
систем, входные и выходные воздействия
у которых представлены в виде сообщений
или сигналов.

В
основе метода лежит понятие агрегата
как элемента системы. Математическая
модель агрегата выражается в виде
зависимостей (1.5) с конкретизацией
входных воздействий, состояний и
операторов выходов и переходов. В
частности, выделяют особые состояния
агрегата, например, получение входного
или управляющего сигнала или выдача
выходного сигнала. Из особого состояния
агрегат скачкообразно может переходить
в новое состояние. Выделяются отдельные
операторы перехода для случая
поступления в агрегат входного сигнала
V`, управляющего сигнала V,
входного и управляющего сигналов V, вида
случайных выходных сигналов W и изменения
состояния в интервалах между особыми
состояниями U.

Агрегативная
система образуется при расчленении
систем на элементы, каждый из которых
представляет собой агрегат.

Описание
исследуемых объектов в виде агрегативных
систем позволяет использовать
универсальные средства имитационного
моделирования.

2)
Кусочно-линейные агрегаты. Дальнейшая
конкретизация структуры состояний,
входных и выходных воздействий,
операторов переходов и выходов приводит
к понятию кусочно-линейных агрегатов,
удобных для формализации разнообразных
процессов. В основе этого подхода лежит
кусочно-линейный закон изменения
состояний системы, что обеспечивает
простоту вычисления опорных моментов
времени и реализации модели системы.
Для кусочно-агрегативных систем в
частных случаях результаты можно
получить путем применения аналитического
метода.

3)
Управляющие последовательности. Метод
заключается в том, что функционирование
системы определяется управляющими
последовательностями, имеющими
определенный физический смысл, и
алгоритмами, описывающими управление
системой с помощью введенных
последовательностей. Управляющие
последовательности и алгоритмы позволяют
составлять рекуррентные соотношения
для описания функционирования
кусочно-линейного агрегата.

4)
Стохастические сети. Используются для
описания стохастических систем с
дискретным множеством состояний,
входных и выходных воздействий,
функционирующих в непрерывном времени.
Стохастическая сеть – это совокупность
систем массового обслуживания (СМО),
в которой циркулируют заявки, переходящие
из одной системы в другую. Стохастическая
сеть при определенных условиях может
рассматриваться как совокупность
независимых СМО, что дает возможность
применять теорию массового обслуживания
для проведения аналитического
моделирования.

5)
Системы массового обслуживания. В основе
СМО лежит понятие устройства, которое
может выполнять конечное множество
операций при возникновении требования
(заявки) на выполнение операции. Если
устройство выполняет любую операцию,
считается, что оно занято (работает),
в противном случае устройство свободно.
Такое описание системы как устройства
с ограниченным числом состояний дает
еще большую абстракцию, чем понятие
агрегата.

Временная
последовательность заявок называется
потоком заявок. Общий поток заявок
может состоять из нескольких потоков.
В случае независимости потоков,
случайных моментов наступления или
завершения обслуживания заявок в
системе могут возникать очереди.
Очередь — это заявки ожидающие
обслуживания, когда устройство занято.
Совокупность устройства, потоков
заявок и очередей к нему и называют
системой массового обслуживания.

Теория
массового обслуживания широко
разработана и нашла применение при
моделировании ВС.

6)
Непрерывные детерминированные системы.
Если в модели не учитывается воздействие
случайных факторов, а операторы
переходов и выходов непрерывны, то
зависимости (1.5) можно представить в
виде дифференциальных уравнений:

_{=h(Z(t),X(t),t);

(1.6)}

_{y=g(Z(t),t);

(1.7)}

где
h,g-векторы
функций состояний и выходов;

X,Y,Z-векторы
входных воздействий, состояний и
выходных воздействий соответственно.

Для
линейных систем, когда операторы
переходов и выходов однородны и аддитивны,
соотношения (1.6) и (1.7) упрощаются и
проводится исследование аналитическими
или численными методами.

Подобные
математические модели используются
при анализе функциональных элементов
и электрических устройств ВС.

7)Автоматы.
Рассмотренные выше формализованные
математические схемы пригодны для
систем, функционирующих в непрерывном
времени. Системы, состояния которых
определены в дискретные моменты
времени t₀,t₁,…,
получили название автоматов. В каждый
дискретный момент времени в автомат
поступает входной сигнал X(t), под
действием которого автомат переходит
в новое состояние в соответствии с
функцией переходов

Z(t)
= _a(Z(t-1),X(t)),
и выдает выходной сигнал в соответствии
с функцией выходов Y(t) = _a(Z(t-1),X(t)).

Если
автомат характеризуется конечным
множеством состояний, входных и
выходных сигналов, он называется
конечным.

8)Вероятностные
автоматы. Эти модели используются для
описания стохастических систем,
функционирующих в дискретном времени.
Функции переходов и выходов такого
автомата определяют распределение
вероятностей на множестве состояний
и выходных сигналов соответственно.
Функционирование вероятностного
автомата описывается с помощью цепей
Маркова. Для оценки характеристик
систем, представляемых в виде автомата,
могут использоваться аналитические
или имитационные методы.

Кроме
приведенных математических схем для
формализованного описания работы систем
используется бинарная алгебра, сети
Петри, Е-сети и др.

Если
невозможно построить математическую
модель всей системы, математические
модели создаются для отдельных элементов,
а для всей системы строится
программно-алгоритмическая модель.

1.3.5 Выбор метода моделирования

Разработанная
математическая модель может быть
исследована аналитическими или
имитационными методами.

Аналитический
метод дает наиболее полное исследование
модели, в некоторых случаях с применением
методов оптимизации. Для исследования
модели аналитическим методом математическую
модель необходимо преобразовать к
явному виду зависимостей характеристик
и параметров системы и внешних
воздействий. Аналитический метод
исследования используется обычно для
первоначальной грубой оценки
характеристик всей системы или отдельных
подсистем, а также на ранних стадиях
проектирования, когда нет информации
для более точного построения модели.

Если
модель не поддается исследованию
известными аналитическими методами,
целесообразно применять численные
методы, которые могут использоваться
для более широкого класса систем.
Результатом исследования систем
численными методами являются таблицы
значений искомых величин для конечного
набора значений параметров и нагрузки.

Для
моделирования можно применять
качественные методы, если аналитическими
и численными методами полученные
уравнения решить нельзя. Эти методы
позволяют оценивать приближения
искомых величин и поведение системы
в целом. Важность качественных методов
возрастает с увеличением сложности
систем.

Наиболее
универсальным методом исследования
систем и количественной оценки их
характеристик является имитационное
моделирование (ИМ), при котором
динамические процессы системы
заменяются имитационными процессами
в абстрактной модели, но с сохранением
длительностей и временных последовательностей
отдельных операций. Поэтому метод ИМ
мог бы называться алгоритмическим или
операционным. В процессе имитации, как
при эксперименте с оригиналом, фиксируются
определенные события и состояния или
изменяются выходные воздействия, по
которым вычисляются характеристики
качества функционирования системы.

ИМ
позволяет рассматривать процессы,
происходящие в системе, на любом уровне
детализации. Используя алгоритмические
возможности ВС, в имитационной модели
можно реализовать любой алгоритм
управления или функционирования.
Имитационными методами могут исследоваться
и модели, допускающие аналитическое
исследование. Потому имитационные
методы являются основными методами
моделирования сложных систем.

Методы
ИМ различаются в зависимости от класса
исследуемых систем, вида параметров
системы и внешних воздействий и способов
задания модельного времени.

В
первую очередь различают методы ИМ
дискретных и непрерывных систем. К
дискретным относятся системы с
дискретным изменением состояний, т.е.
системы, имеющие конечное множество
состояний, переход между которыми
происходит мгновенно. Непрерывная
система — это система, состояния которой
изменяются постепенно, принимая
бесконечное множество значений. У
непрерывных систем могут быть искусственно
выделены определенные состояния
элементов, например, некоторые характерные
значения переменных фиксируются как
достижение определенных состояний.
При моделировании ВС на системном уровне
их удобно рассматривать как системы с
дискретным изменением состояний.

Одним
из основных параметров при ИМ является
модельное время, которое отображает
время функционирования реальной
системы. В зависимости от способа
продвижения модельного времени
различают методы моделирования с
приращением временного интервала и
методы с продвижением времени до особых
состояний. В первом случае модельное
время продвигается на величину t
и определяются изменения состояний
элементов и выходных воздействий
системы, которые произошли за это
время. После этого модельное время
продвигается на t
и процедура повторяется и т.д. до конца
периода моделирования Т_m;
t
обычно постоянно, но может быть и
переменным. Этот метод называют
моделированием по принципу “t”.
Во втором случае в текущий момент
модельного времени t сначала анализируются
будущие особые состояния — поступление
дискретных входных воздействий,
завершение обслуживания и т.п., и
определяется их начало t_i>t.
Затем выбирается наиболее раннее
особое состояние и модельное время
продвигается до момента наступления
этого состояния. Между двумя особыми
состояниями система не изменяет своего
состояния. Затем анализируется реакция
системы на выбранное особое состояние
(например, определяется момент
наступления следующего особого
состояния) и модельное время продвигается
до будущего особого состояния. Процесс
повторяется до завершения модельного
времени T_m.
Этот метод называют моделированием по
принципу особых состояний или принципу
“z”.
Метод позволяет экономить машинное
время моделирования, но используется
только тогда, когда возможно определение
моментов наступления будущих особых
состояний.

По
значениям количественных параметров
системы (детерминированные или случайные)
различают моделирование детерминированное
и статистическое. При статистическом
моделировании для получения достоверных
вероятностных характеристик процессов
функционирования системы требуется их
многократное воспроизведение с различными
конкретными значениями случайных
факторов и статистической обработкой
результатов измерений . В основу
статистического моделирования положен
метод статических испытаний — метод
Монте-Карло.

Особое
значение при статистическом
моделировании имеет нестационарность
переменных и внешних воздействий
системы. В этом случае должны быть
использованы специальные методы
моделирования, в частности, метод
повторных экспериментов.

Еще
одним классификационным параметром
считается схема формализации,
принятая при создании математической
модели. Различают методы моделирования,
ориентированные на алгоритмический
(программный) или структурный
(агрегатный) подход. В первом случае
процессы управляют элементами системы,
во втором — элементы управляют
процессами, определяющими порядок
функционирования системы.

Таким
образом, выбор метода моделирования
полностью определяется математической
моделью и исходными данными.

1.3.6. Выбор средств моделирования

После
выбора метода моделирования необходимо
выбрать технические и программные
средства для проведения моделирования.
В качестве программных средств
могут быть использованы алгоритмические
языки или автоматизированные системы
моделирования.

1.
Алгоритмические языки. Для создания
программных моделей могут использоваться
любые универсальные алгоритмические
языки общего назначения, имеющие средства
для реализации параллельных алгоритмов
и динамического распределения памяти.

Достоинством
использования указанного типа языков
для ИМ является возможность применения
стандартного программного обеспечения,
построение быстродействующих и
экономичных по затратам памяти
программных моделей, учет детальных
особенностей функционирования
моделируемых систем.

2.
Языки моделирования. Для облегчения
решения задач, характерных для ИМ,
таких, как организация псевдопараллельных
вычислений, динамическое распределение
памяти, операции с модельным временем,
отображающим время функционирования
оригинала, имитации случайных процессов
ведения массива событий и т.п. созданы
специальные проблемно-ориентированные
средства (программные системы), которые
называют языками моделирования.

По
структуре и правилам использования
программные языки моделирования
подобны универсальным алгоритмическим
языкам: они имеют набор операторов,
сопровождаемых соответствующими
операндами. Но операторы языков
моделирования предполагают выполнение
более сложных процедур, что упрощает
составление программной модели. Это
языки более высокого уровня, чем
алгоритмические.

В
настоящее время известно более 500 языков
моделирования, что обусловлено
разнообразием классов моделируемых
систем, методов математического описания,
целей и методов моделирования.

Языки
моделирования подразделяются на языки
моделирования дискретных, непрерывных
и комбинированных систем.

3.
Автоматизированные системы моделирования.
С целью дальнейшего упрощения и
ускорения создания машинных моделей
были созданы автоматизированные системы
моделирования, которые обеспечивают
автоматическое создание программной
модели по одной из формализованных
схем на основе задаваемых параметров
системы, внешних воздействий и
особенностей функционирования. По
результатам машинного эксперимента
основные выходные данные вычисляются
и выводятся автоматически, дополнительные
— по специальному указанию. Такие
системы называют универсальными
автоматизированными имитационными
моделями или имитационными программами.

Технические
средства моделирования – это
универсальные или специализированные
ВС. Основным требованием, предъявляемым
к универсальным ВС, используемым для
ИМ, является наличие оперативной
памяти достаточно большой емкости, т.к.
в процессе моделирования производится
многократное обращение к параметрам
элементов и воздействий (статическим
и динамическим). Например, при
моделировании системы, состоящей из
20 — 30 элементов емкость оперативной
памяти должна быть не менее 100 Кбайт.

При
статистическом моделировании
каждый эксперимент требует существенных
затрат машинного времени, потому
желательно использовать для моделирования
высокопроизводительные ВС. Остальные
требования к составу и характеристикам
универсальных ВС не являются существенными.
К специальным техническим средствам
аналитического моделирования относятся
аналоговые вычислительные машины,
используемые для исследования
непрерывных детерминированных систем.

В
связи с широким применением ИМ в
различных областях, разрабатываются
и выпускаются специальные ВС, такие,
как стохастические машины, машины
имитационного моделирования, гибридные
моделирующие комплексы.

Программные
и технические средства моделирования
выбираются с учетом нескольких
критериев:

1) достаточность и полнота средств для
реализации концептуальной и математической
моделей;

2) доступность , простота и легкое
освоение программных средств
моделирования;

3) быстрота и точность создания модели.

После
выбора средств моделирования создается
программная модель, т.е. разрабатывается
алгоритм, конкретизируется форма
представления данных и результатов,
проводится написание и отладка программы.

1.3.7.Проверка адекватности и корректировка
модели

Проверка
адекватности модели заключается в
оценки ее соразмерности с исследуемой
системой, а также равнозначности системе.
Однако, модель не должна быть полным
отображением системы, так как при этом
теряется смысл ее создания.

В
процессе создания модели адекватность
нарушается в результате стратификации,
детализации, локализации; из-за идеализации
внешних условий и режимов функционирования,
исключения тех или иных параметров,
пренебрежения случайными факторами.
Принятые аппроксимации, предположения
и гипотезы также уменьшают соответствие
между системой и моделью. По этим причинам
результаты моделирования будут
существенно отличаться от реальных.

Естественной
простейшей мерой адекватности модели
служит отклонение некоторой характеристики

оригинала от соответствующей
характеристики модели
:

или
в относительных единицах:

Считается,
что модель адекватна системе, если
вероятность того, что отклонение

не превышает предельной величины
,
больше допустимой вероятности
:

Практическое
использование этого критерия затруднено
по следующим причинам: во-первых, для
проектируемых моделируемых систем
отсутствует информация о значении
;
во-вторых, система оценивается по
множеству характеристик, у которых
могут быть разные величины отклонения;
в-третьих, если характеристики — случайные
величины и функциями и нестационарные,
то для них результаты моделирования
могут быть более точными, чем для
оригинала из-за большого числа реализаций;
в-четвертых, отсутствует возможность
априорного точного задания предельных
отклонений

и допустимых вероятностей
.

На
практике оценка адекватности проводится
путем следующих проверок:

проверка
моделей внешних взаимодействий (оценка
математическими методами предположений,
аппроксимаций, гипотез);
проверка
концептуальной модели (выявляются
ошибки постановки задачи);
проверка
математической модели;
проверка
способов измерения и вычисления выходных
характеристик (выявляются ошибочные
решения);
проверка
программной модели (анализируется
соответствие операций и алгоритмов
функционирования программной и
математической модели, проводятся
контрольные расчеты при типовых и
предметных значениях переменных,
выявляются инструментальные ошибки
программирования).

По
результатам проверки адекватности
выявляются несоответствия модели
системе и проводятся изменения модели
по типам: глобальные, локальные и
параметрические.

Глобальные изменения проводятся в
случае, если в концептуальной или
математической модели имеются методические
ошибки. Устранение таких ошибок приводит
к разработке новой модели.

Локальные
изменения связаны с уточнением некоторых
параметров или алгоритмов. Они выполняются
путем замены моделей компонентов системы
и внешних воздействий на эквивалентные,
но более точные модели. Локальные
изменения требуют частичного изменения
математических моделей, но могут привести
к необходимости разработки новой
программной модели. Для уменьшения
вероятности проведения таких изменений
модель желательно разрабатывать с
большей степенью детализации, чем это
необходимо для достижения целей
моделирования.

К
параметрическим относятся изменения
некоторых специальных параметров,
называемых калибровочными. Для повышения
адекватности модели путем параметрических
изменений необходимо заранее выявить
калибровочные параметры и способы
варьирования ими.

Корректировка
модели проводится в таком порядке:
глобальные изменения, локальные и
параметрические.

1.3.8. Планирование экспериментов с моделью

Цели
моделирования достигаются при исследовании
разработанной модели путем проведения
экспериментов, в результате которых
определяются выходные характеристики
при различных значениях переменных
параметров модели. Эксперименты должны
проводиться по определенному плану.
Особую важность планирование приобретает
при численном и статистическом
имитационном моделировании на
универсальных вычислительных системах,
так как число возможных сочетаний
управляемых параметров может быть
большим, а каждый машинный эксперимент
проводится при определенном сочетании
значений параметров. Например, при пяти
управляемых параметрах, каждый из
которых может имеет три значения,
количество сочетаний параметров равно
243, при десяти параметрах (по 5 значений
каждого) число сочетаний приближается
к 10 млн. При ограниченных временных и
вычислительных ресурсах не представляется
возможным провести все эксперименты.
Возникает необходимость в выборе
определенных сочетаний параметров и
последовательности проведения
экспериментов. Это процедура называется
стратегическим
планированием.

Разработка
плана начинается на ранних этапах
создания модели, когда выявляются
характерные параметры, с помощью которых
предполагается управлять качеством
функционирования системы. Эти параметры
называют факторами.
Затем выделяются возможные значения
количественных параметров и варианты
качественных параметров — уровни
q. При этом число
экспериментов

где
к — число
факторов.

Особенно
тщательно нужно планировать эксперименты
при исследовании нестационарных систем,
так как в этом случае требуется
избирательное увеличение числа
экспериментов.

Методы
уменьшения длительности машинного
эксперимента при обеспечении достоверности
результатов ИМ получили название
тактического планирования.
На длительность одного эксперимента

влияет степень стационарности системы,
взаимозависимости характеристик и
значения начальных условий моделирования.

Данные,
собранные в эксперименте, могут
рассматриваться как временные ряды,
состоящие из замеров определенных
характеристик. Ряд замеров характеристики
y может
рассматриваться как выборка из
стохастической последовательности.
Если же последовательность стационарна,
ее среднее

не зависит от времени. Оценкой

является среднее по временному ряду
.

Если
заданы максимально допустимая ошибка
оценки доверительного интервала и
минимальная вероятность того, что
истинное среднее

лежит внутри этого интервала, то
существует минимальный размер исследуемой
выборки, соответствующий минимальной
длительности эксперимента. Для оценки
нескольких характеристик период
моделирования определяется по
максимальному значению. Требуемый
размер выборки зависит от дисперсии
оцениваемой характеристики. Чем больше

,
тем больше должен быть размер выборки.
Для коррелированных случайных
характеристик следует оценивать
дисперсию. Существуют специальные
методы обработки результатов моделирования,
использующие априорную информацию о
системе и позволяющие уменьшить размер
выборки при сохранении заданной точности
оценок. К ним относятся методы
коррелированных, стратифицированных
выборок и т.д.

Большинство
имитационных моделей используются для
изучения уже установившихся равновесных
режимов функционирования систем, но в
начальный период работы системы имеется
переходный режим, длительность которого
может быть большой. Значения выходных
характеристик, измеренных в этот период,
смещают их общие оценки.

Существуют
три метода уменьшения ошибок начальных
условий. Первый состоит в увеличении
периода моделирования, т.к. с увеличением
числа замеров влияние начального
смещения на статистическую оценку
стремится к нулю. Второй метод состоит
в переносе начала сбора статистики с
начального момента времени. Третий
метод заключается в задании характеристик
и параметров моделей не с “нулевого”,
а специально заданного состояния,
близкого к установившемуся.

При
моделировании нестационарных процессов
установившийся режим полностью
отсутствует. Естественным методом
определения характеристик ИМ нестационарной
системы является метод повторных
экспериментов, что приводит к особым
методам по их планированию.

1.3.9. Анализ результатов моделирования

Анализ
результатов моделирования включает
несколько этапов.

1.
Обработка измерений. При статистическом
моделировании измеряются множество
значений по каждой выходной характеристике,
т.е. выборки, которые необходимо
обрабатывать. Обработка случайных
характеристик заключается в вычислении
оценок математического ожидания,
дисперсии и корреляционных моментов.
Эти оценки должны быть состоятельными,
несмещенными и эффективными. Обработку
проводят по рекуррентным формулам,
чтобы исключить необходимость хранения
в памяти ЭВМ результатов всех измерений.
Для вероятностных характеристик строятся
эмпирические плотности распределений
вероятностей в виде гистограмм, для
построения которых весь интервал
предполагаемых значений характеристики
y
разбивается на подинтервалы и в ходе
измерений определяют число попаданий
характеристики в каждый интервал; по
полученным данным строится гистограмма
распределения, к которой впоследствии
можно подобрать и теоретический закон
распределения.

Если
искомая характеристика является
случайной стационарной и эргодичной
функцией времени, то для нее вычисление
средней оценки по времени заменяется
средним по множеству измерений для
одного продолжительного эксперимента.
Если характеристика нестационарная,
то период

разбивается на отрезки с постоянным
шагом

и запоминается значение характеристик
в конце каждого отрезка. Проводится
серия экспериментов и измерения на
каждом отрезке обрабатываются как при
оценке случайных величин.

2.
Определение зависимостей характеристик
от параметров системы. Для получения
этих зависимостей используются:
корреляционные, дисперсионные или
регрессионные методы. С помощью
корреляционного анализа устанавливаются
связи между случайными величинами,
оценкой которых служит коэффициент
корреляции при линейной связи между
величинами и нормальным законом их
совместного распределения. Дисперсионный
анализ используется для установления
относительного влияния различных
факторов на значения выходных
характеристик. Методы регрессионного
анализа используются, когда можно найти
аналитические зависимости между
характеристиками и факторами. Регрессионный
анализ заключается в том, что выбирается
вид соотношений между зависимыми и
независимыми переменными, по
экспериментальным данным вычисляются
параметры выбранной зависимости и
оценивается качество аппроксимации
экспериментальных данных моделью. Если
качество неудовлетворительное, берется
зависимость другого вида и процедура
повторяется. Анализ результатов
моделирования позволяет уточнить
множество информативных параметров
модели, а впоследствии провести
существенное изменение концептуальной
модели, а также найти функциональные
зависимости характеристик и параметров
с последующем созданием аналитической
модели системы.

3.
Использование результатов моделирования.
Результаты моделирования используются
в конечном счете для принятия решения
о работоспособности системы или для
оптимизации системы. Решение о
работоспособности принимается по
изменению характеристик системы в
установленных границах при любых
изменениях параметров. Наиболее общей
и сложной является задача оптимизации
системы: требуется найти такое сочетание
значений переменных параметров из
множества допустимых, которое максимизирует
значение критерия эффективности:

при
соблюдении ограничений
.

Для
случайных величин задача оптимизации
ставится так:

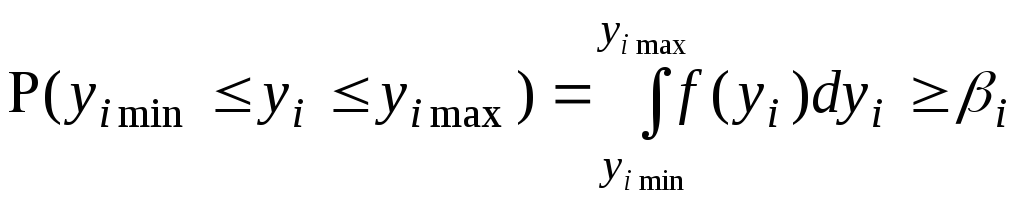
где

— максимально допустимая вероятность
того, что конкретные значения

не выйдут за заданные пределы.

При
большом количестве сочетаний параметров
поиск оптимального варианта требует
использования методов математического
программирования.

Контрольные вопросы к разделу 1:

Что такое
моделирование?
Что понимается
под словом “модель”?
Как выполняется
классификация моделей?
Каковы
основные этапы моделирования?
В чем
заключается этап постановки целей
моделирования?
Как строится
концептуальная модель системы?
В чем состоит
подготовка данных для моделирования?
Какие
математические модели используются
при моделировании ВС?
Как проводится
выбор метода моделирования?
Как выбираются
средства моделирования?
Какие
изменения могут вноситься в модель в
процессе проверки адекватности и
корректировки?
В чем
заключается обработка и анализ
результатов моделирования?

Источник

Сценарное моделирование (планирование) – это один из наиболее эффективных системных инструментов стратегического менеджмента вообще и стратегического анализа в частности.

Исторически сценарии возникли примерно 30 лет назад в качестве альтернативы одновариантных прогнозов будущего развития конкретных компаний.

Одновариантные прогнозы, как правило, довольно жестко задавали по существу единственную траекторию будущего развития организации. На практике (особенно в условиях изменчивой внешней среды) они очень часто оказывались ошибочными.

Поэтому при сценарном подходе для конкретной организации стали разрабатывать несколько примерно одинаково вероятных, но значимо контрастных вариантов будущего развития ее внешней среды. Они были инструментами именно корпоративной стратегии, и в них делался акцент как раз на тех позициях, которые являлись значимыми для менеджеров организации при принятии стратегических решений.

Особую роль в становлении высококачественного сценарного моделирования, так же как и для обеспечения эффективного стратегического менеджмента в целом, может сыграть система так называемых стратегических бесед ( strategic conversations). Один из результативных способов построения системы стратегических бесед – это проведение в организации серии адекватных бесед-диалогов между соответствующими менеджерами и специалистами в процессе освоения и развития метода сценарного планирования.

Задача сценарного метода – выработать некоторое общее понимание в коммерческой организации, которое позволит ее персоналу согласованно действовать для достижения главных стратегических целей организации.

Важнейшая цель всей системы стратегических бесед – создание и развитие в организации процесса ее стратегического самообучения. Стратегические беседы могут представлять собой одну из форм превращения коммерческой организации в обучающуюся организацию.

В качестве исходной основы практического построения системы стратегических бесед предлагаются рекомендации по созданию эффективного процесса сценарного моделирования.

Восемь шагов методики

В данном разделе предлагаются рекомендации по восьмишаговой методике осуществления процесса сценарного моделирования (планирования).Внимательное ознакомление с методическими рекомендациями даст вам более глубокое и конструктивное представление о сценарном моделировании.

Шаг 1. Определение ключевых стратегических направлений и/или вопросов.На первом этапе процесса сценарного моделирования прежде всего надо собрать все результаты и данные стратегического анализа как внешней, так и внутренней среды организации, которые в ней уже имеются на момент начала разработки сценариев.

Полный перечень конкретных формулировок всех таких направлений и решений должен интегрировать и специфику бизнеса организации, и специфику заданного сценарного периода с точки зрения интересов именно данной конкретной организации.

С одной стороны, совершенно ясно, что указанный перечень надо установить, но, с другой стороны, столь же очевидно, что сделать это практически непросто. Поэтому предлагаются следующие рекомендации.

Под руководством первого менеджера организации рекомендуется опросить топ-менеджеров и обсудить наиболее актуальные и важные стратегические вопросы, стоящие перед организацией на текущий момент. Например:

Должна ли наша организация в течение ближайшего года запустить в действие новое направление в сети реализации профильных продуктов или в области НИОКР либо открыть новый филиал?
Надо ли нам приобретать активы в новой отрасли бизнеса?
Начинать ли практическое осуществление таких крупных проектов, как Проект 1 и Проект 2, или пока воздержаться, или вообще от них уже стоит отказаться?

При наличии данных, команда разработчиков сценариев:

проводит специальное целевое исследование на предмет определения всех возможных направлений развития бизнеса на конкретный сценарный период;
анализируются все ключевые стратегические решения, которые организация собирается принять с учетом разрабатываемых сценариев.

Шаг 2. Установление ключевых факторов ближней внешней среды.На втором этапе фиксируются и анализируются ключевые факторы из ближней внешней среды организации, которые определяют успех или неудачу по каждому из направлений, установленному на Шаге 1, а также выявленные на Шаге 1 стратегические вопросы.Такие факторы устанавливаются по внешней среды организации, ее потребителям и конкурентам.

Основной вопрос, на который в каждом сценарии должен содержаться ответ по каждому вопросу Шага 1: что должны знать менеджеры организации, которые принимают стратегические решения, чтобы делать осознанный выбор того или иного варианта решения?

Шаг 3. Определение ключевых факторов дальней внешней среды.На этом этапе выявляют и углубленно анализируют ключевые факторы внешней среды организации, которые определяют действие факторов, установленных на Шаге 2. Причем на этом уровне должны быть определены все ключевые факторы, которые влияют на данную организацию именно через факторы Шага 2.

Некоторые из таких факторов внешней среды организации являются вполне предопределенными (например, демографические тенденции), другие – неопределенными (например, результаты выборов главы государства). На Шаге 3 очень важно и полезно установить, что конкретно по ключевым факторам дальней внешней среды в будущем произойдет обязательно, а что может произойти случайно.

В исследовательском плане данный шаг является самым интенсивным и сложным.Обусловлено это тем, что, во-первых, надо представить несколько вариантов возможного изменения ключевых факторов уровня дальней внешней среды (Шаг 3) с учетом соответствующих последствий в данной среде как сложной и динамичной системе. Во-вторых, надо представить, как изменения уровня дальней внешней среды изменят ключевые факторы уровня ближней внешней среды (Шаг 2). В-третьих, вариантную динамику ключевых факторов Шага 2 надо представить и описать таким образом, чтобы соответствующая информация позволяла качественно решать стратегические вопросы Шага 1.

Шаг 4. Ранжирование по важности и степени неопределенности.На этом этапе проводится ранжирование всех факторов Шага 3 и Шага 2 по двум критериям:

Важность каждого фактора указанных уровней для принятия стратегических решений Шага 1.
Степень неопределенности по факторам Шага 3 и Шага 2 для решения стратегических вопросов Шага 1.

Основная задача Шага 4 – определение основных факторов по каждому критерию, т. е отдельно двух-трех факторов, которые являются самыми важными, и отдельно двух-трех самых неопределенных факторов.

Сценарии не могут различаться по предопределенным факторам, ибо во всех сценариях такие факторы действуют одинаково. То есть сценарии будут существенно различаться именно по факторам и тенденциям, которые выявлены на Шаге 4.

Шаг 5. Выявление логики каждого сценария.Результатом данного этапа должны стать так называемые «логические стержни», т. е. альтернативные логики развития каждого сценария.

Цель Шага 5 состоит в том, чтобы в соответствии с разными логическими стержнями выйти на относительно небольшое число сценариев, которые являются разными по критерию содержания решений, которые должны приниматься по стратегическим вопросам Шага 1.

При удачной разработке различных сценариев они должны показывать положительные результаты, т. е. определенный бизнес-успех от принятия соответствующих стратегических решений Шага 1.

При любом уровне неопределенности разных сценариев все равно должно быть немного, в идеале – не более четырех.

В рамках каждого сценария собственно динамический аспект логики его развития определяется как особенный – так называемый сценарный драйвер.В зависимости от числа сценарных драйверов получается соответствующее многообразие конкретных сценариев. При одном сценарном драйвере – линейный спектр, при двух – матрица, при трех – куб и т. д.

Пример. Допустим, что для автомобилестроительной компании в рассматриваемом стратегическом периоде сценарными драйверами являются цена на бензин и политика государственного протекционизма. Тогда оказываются возможными четыре сценария, соответствующие четырем разным логикам:

Сценарий – 1. Высокие цены на бензин устанавливаются в условиях повсеместного протекционизма. В таком случае конкурентное преимущество будут иметь местные производители малолитражных машин, т.е. экономичных по фактору бензина автомобилей.
Сценарий – 2. Высокие цены на бензин устанавливаются в условиях отсутствия на глобальном рынке протекционистских барьеров. В такой ситуации на глобальном рынке будет доминировать импорт автомашин, которые являются наиболее конкурентоспособными по фактору использования дорогого бензина.
Сценарий – 3. Низкие цены на бензин назначаются в условиях протекционизма. Тогда, например, американские автомобили, которые потребляют много бензина, будут иметь хороший сбыт в США, но не за рубежом.
Сценарий – 4. Низкие цены на бензин устанавливаются в условиях открытого глобального рынка. В подобной ситуации экономичные автомашины будут достаточно интенсивно конкурировать между собой по всему миру, но при этом большие автомобили (не малолитражки) станут находить спрос и на зарубежных рынках.

Чем меньше число явно доминирующих сценарных драйверов, тем прозрачнее логики соответствующих сценариев и тем четче альтернативный выбор при принятии стратегических решений Шага 1.

Шаг 6. «Очистка» сценариев.На данном этапе, т. е. в ситуации, когда установлены наиболее важные факторы-драйверы, которые задают логику развития различных сценариев, надо вернуться к ключевым факторам Шага 3 и Шага 2.

Каждому фактору и/или тенденции указанных уровней в каждом сценарии надо уделить особое внимание. То есть такие факторы по каждому сценарию должны стать предметом отдельного целевого исследования.

Шаг 7. Выводы.На седьмом этапе, т. е. когда все сценарии уже разработаны достаточно детально, самое время вернуться к ключевым стратегическим вопросам Шага 1, чтобы посмотреть, как будет выглядеть то или иное решение в рамках каждого сценария.

Главная цель данного этапа – оценка устойчивости как отдельных возможных стратегических решений Шага 1, так и в целом соответствующих стратегий развития организации относительно всех разработанных сценариев.

В идеале каждое стратегическое решение и стратегия организации в целом должны быть достаточно устойчивыми при каждом сценарии. Выйти на такие решения весьма сложно, а во многих случаях невозможно в принципе. Более типичной является ситуация, когда определенные стратегические решения и/или стратегия в целом оказываются хорошими при одном или нескольких конкретных сценариях и плохими – при других сценариях

Поэтому при обосновании тех или иных решений Шага 1 необходимо оценивать (взвешивать) риски, связанные с вероятностью наступления тех или иных сценариев. Кроме того, должен вестись осознанный поиск именно таких стратегических решений, которые станут достаточно приемлемыми для организации относительно всех разработанных сценариев.

Шаг 8. Определение характерных индикаторов.Представляется очевидным, что по мере развития фактических событий желательно как можно раньше узнавать, какой конкретный сценарий из всех разработанных оказался ближе всех к реальной жизни. Сигнализировать об этом должны так называемые характерные или лидирующие индикаторы.

Понятно, что само по себе установление таких индикаторов является непростой задачей. Тем не менее, такие затраты целесообразны, так как в случае создания с помощью характерных индикаторов достаточно эффективной системы раннего обнаружения конкретных сценариев соответствующая организация в области своей стратегической компетенции сразу выходит на качественно более высокий уровень. А такая компетенция, в свою очередь, для данной конкретной организации вполне может стать хорошей основой создания ее сильного и именно стратегического конкурентного преимущества.

Автор: Сергей Александрович Попов,
кандидат экономических наук, доцент Института бизнеса и делового администрирования АНХ при Правительстве РФ.
Источник: Опубликовано на Elitarium.Ru

Источник

#статьи

10 авг 2022
0

Моделирование бизнес-процессов: для чего оно нужно и как его провести

Продолжаем погружаться в управление бизнес-процессами. Рассказываем, как смоделировать процессы компании и описать их самостоятельно.

Иллюстрация: Andrea Piacquadio / Pexels / Colowgee для Skillbox Media

Рассказывает просто о сложных вещах из мира бизнеса и управления. До редактуры — пять лет в банке и три — в оценке имущества. Разбирается в Excel, финансах и корпоративной жизни.

Дипломированный специалист по автоматизации бизнес-процессов. Девять лет опыта в бизнесе и консалтинге. Смоделировал более тысячи процессов для торговых и промышленных предприятий. Основатель OkoCRM.

Фото: личный архив Александра Завьялова

Ни один процесс нельзя улучшить, предварительно не описав его. Это касается не только бизнес-процессов больших компаний, но и алгоритмов работы ИП или самозанятых. Прежде чем оптимизировать бизнес-процессы, важно зафиксировать, как они работают, — то есть смоделировать.

О базовых терминах и идеях в области бизнес-процессов мы рассказали в большом гайде. В этой статье разберём подробнее:

что такое моделирование бизнес-процессов и нотации для моделирования;
какие есть подходы к моделированию и кто этим обычно занимается;
как изображают бизнес-процессы;
как самостоятельно описать бизнес-процессы.

Бизнес-процессы — любые операции внутри компании, которые помогают решать бизнес-задачи и зарабатывать. Моделирование бизнес-процессов — описание этих операций и документирование требований к ним.

Ответственные за моделирование разбираются в процессах компании и описывают, кто, что и как делает. Изучают каждую операцию и разбивают её на этапы. Сначала описывают всё это текстом, затем превращают описание в схему.

В профессиональном моделировании бизнес-процессов часто используют нотации. Нотация — это набор правил для графического описания бизнес-моделей. Нотации описывают:

какие иконки использовать в моделировании и как их читать;
как отображать последовательность действий в процессе и отношения внутри него;
какие элементы обязательно нужно включить.

Нотации нужны для того, чтобы любой человек понимал, что изображено на схеме. Даже если пользователь видит её впервые, он должен разобраться.

Специалисты придумали много вариантов нотаций. Их делят на две основные категории:

Структурные. Они показывают элементы процесса и взаимосвязи между ними. Это нотации стандарта IDEF: IDEF0, IDEF1x, IDEF4, IDEF5.
Динамические. Они показывают логику выполнения процессов, последовательность и варианты их использования. Это нотации DFD, EPC, BPMN.

Ниже, когда мы будем говорить о подходах к моделированию, расскажем о двух вариантах нотаций — IDEF0 и BPMN.

С получившейся моделью бизнес-процесса работают дальше. Двигают элементы так, чтобы корректировать продолжительность цикла, влиять на качество результата или снижать себестоимость. Это называется оптимизацией бизнес-процесса — подробнее о ней говорили в статье. Но прежде чем оптимизировать и улучшать, важно провести качественное моделирование.

В моделировании бизнес-процессов есть три основных подхода: функциональный, процессный и ментальный. В следующих разделах разберём их подробнее.

Иногда можно встретить и другие подходы, но обычно это гибридные решения, собранные из основных. Каждый из трёх подходов предполагает, что процессы нужно визуализировать — рисовать их в виде схем. Различия подходов — в принципах визуализации.

При этом подходе описывают результаты, которые нужно получить, и ресурсы, которые при этом будут задействованы, без учёта последовательности действий.

У модели есть точки входа и выхода: то, что имеем на старте, и то, что хотим получить. Внутри — промежуточные результаты, ресурсы и факторы, которые влияют на процесс.

Задача функционального подхода — показать, какие факторы нужно учесть и какие ресурсы задействовать, чтобы процесс состоялся. Подробного описания действий в этом случае не будет, но появится общее представление о процессе.

Я использую этот подход, чтобы оценить результативность бизнес-процесса, а также для того, чтобы показать свои идеи и варианты решений: от общего к деталям.

На мой взгляд, функциональный подход понятнее всего реализован в нотации IDEF0. Она рассматривает процесс как совокупность логически связанных между собой работ. Нотация показывает, как объекты подчинены друг другу внутри процесса.

Разберём на примере. Пусть это будет изготовление рекламного ролика.

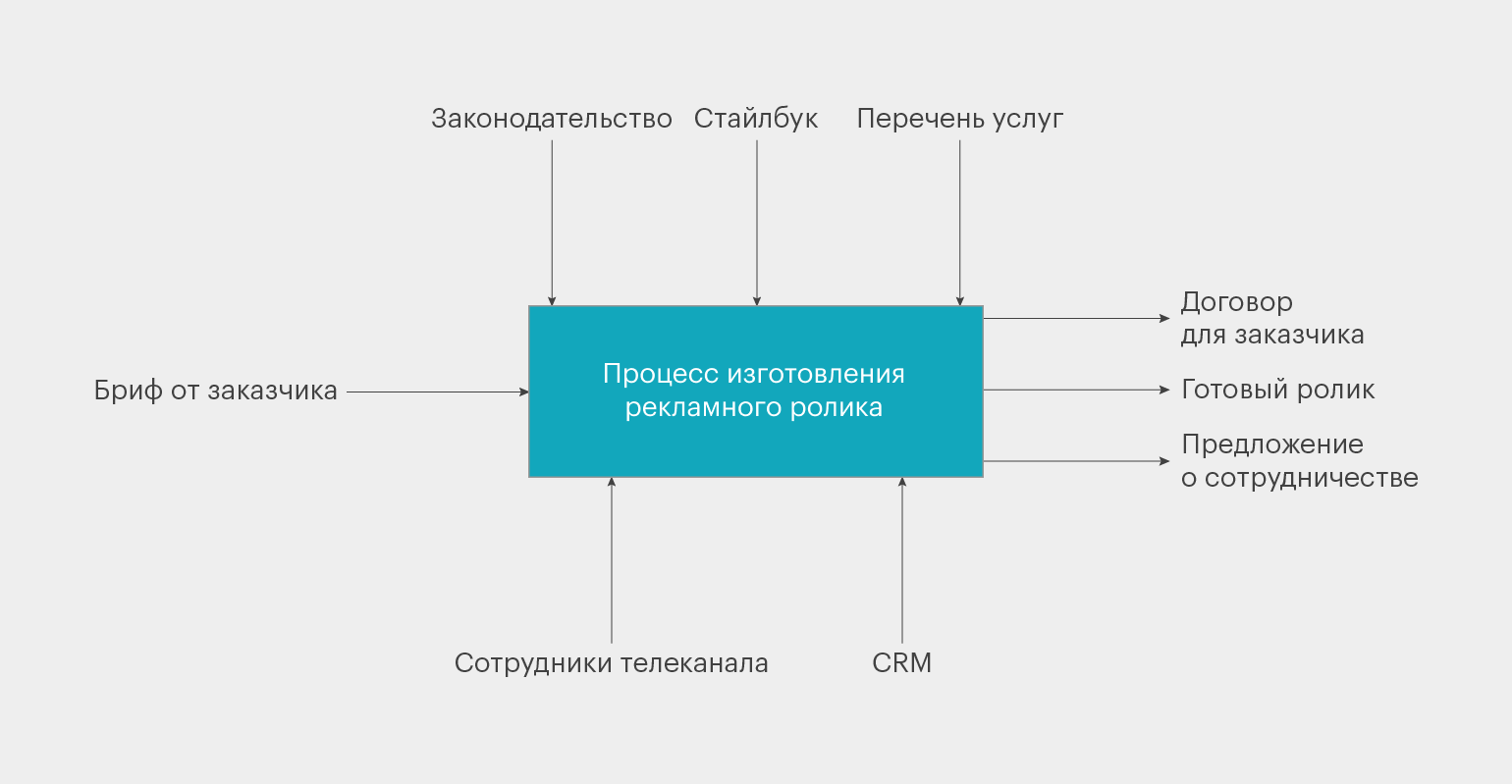
Процесс изготовления рекламного ролика — основной блок с процессами. Я называю его «чёрный ящик». У него есть три входа и один выход:

1. Сверху — вход для информации о контроле и ограничениях. Это данные, которые определяют условия для реализации процесса. Например, при разработке ролика нас будет ограничивать законодательство и стайлбук заказчика. А ещё мы будем опираться на перечень услуг клиента — чтобы в рекламе были корректные данные.

2. Слева — вход для основной информации. На её основе будет создан результат. В примере с роликом, чтобы получить эту информацию, для заказчика проводят брифинг.

О том, как составить бриф для клиента в рекламе и digital, писали в статье.

3. Снизу — вход для механизма, который будет осуществлять функцию. В примере с роликом это CRM, где хранятся данные о заказчике, и сотрудники телеканала, которые будут снимать ролик.

4. Справа — выходы. Это результаты, которые мы получим: заключим договор, снимем ролик и предложим сотрудничать на постоянной основе.

Вот как функция будет выглядеть в виде диаграммы.

Функциональная модель процесса изготовления рекламного ролика
Инфографика: Майя Мальгина для Skillbox Media

В итоге из нескольких таких диаграмм можно собрать одну большую. Важно соблюдать правила расположения данных — сверху, слева и снизу, — чтобы связи между ними сохранялись.

Для неподготовленного управленца это самый понятный подход. Его используют, когда уже определены границы процесса — начало и конец события.

При процессном подходе описывают не результат, а действия, которые необходимо совершить для достижения результата. Процесс можно детализировать сколько угодно — вплоть до операций каждого сотрудника. Получается блок-схема.

Я сторонник процессного подхода. В результате него получаются более прикладные модели, которые понятны и руководителю компании, и исполнителям. Функциональный же подход больше полезен для общего проектирования процессов — и далёк от их практической реализации.

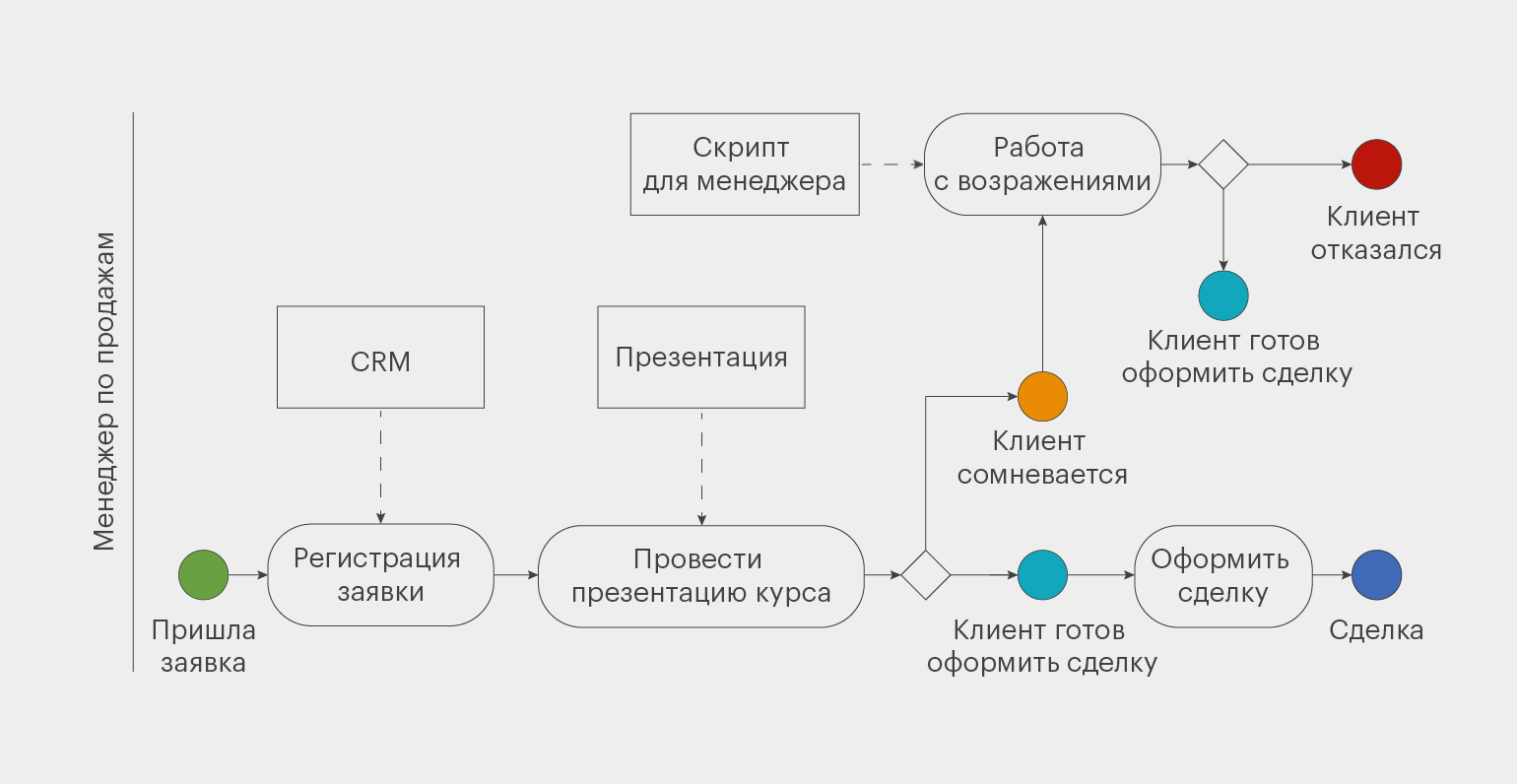
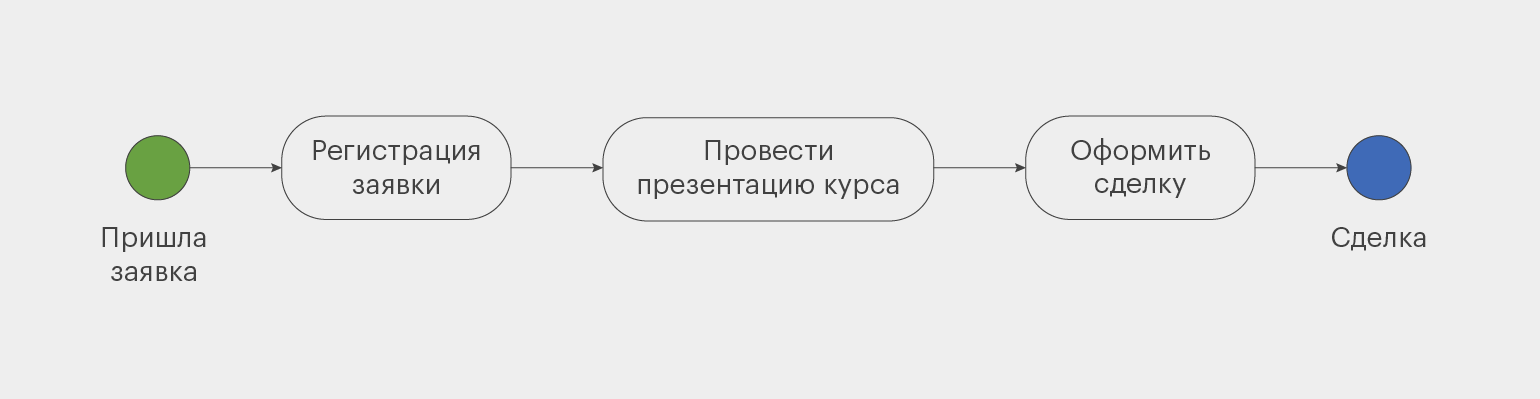
Например, в функциональном подходе «Обработка заявки» — только один из элементов входа. В центре внимания — результат, то есть заключение сделки. В процессном подходе «Обработка заявки» — большой алгоритм. Он подробно описывает действия всей команды.

У процессного подхода есть свои нотации. Стандартом считается BPMN — базовый набор условных обозначений. Его используют для изображения бизнес-процесса в виде блок-схемы.

Нотация BPMN есть в каждом конструкторе для моделирования, но пользоваться ей не обязательно. Гораздо важнее, чтобы схема процесса была читаемой и понятной для руководителя и исполнителей.

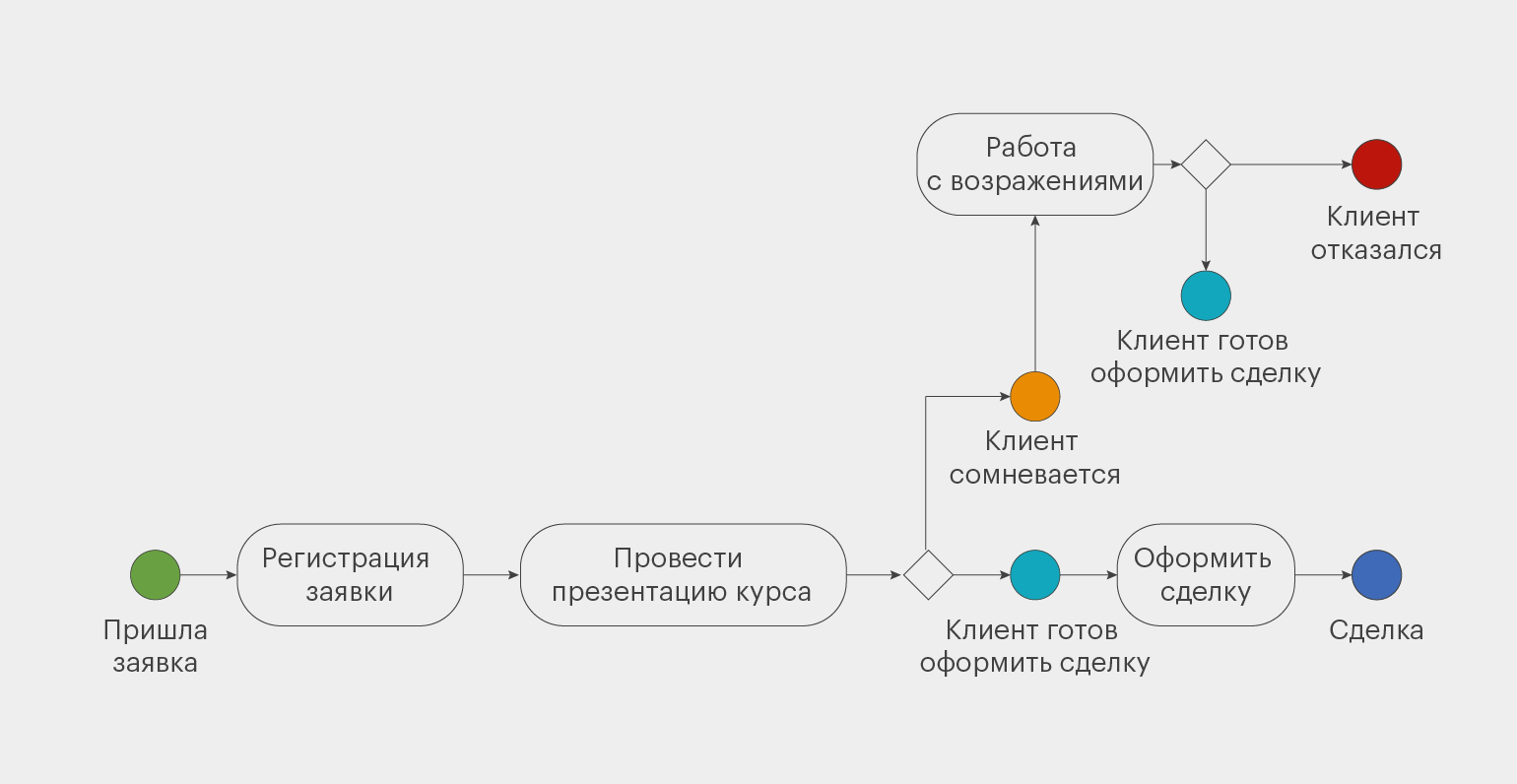
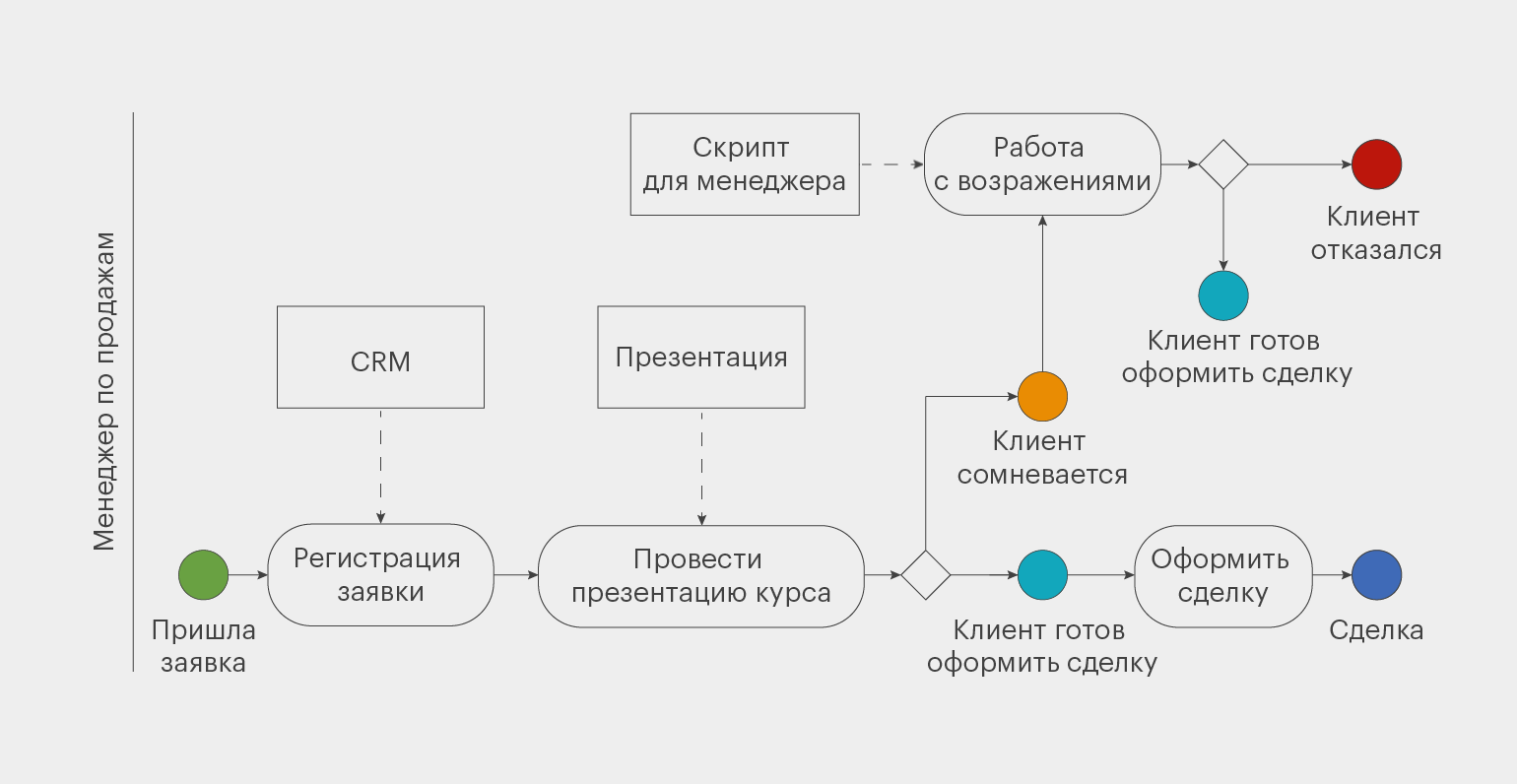
Для примера нарисовали блок-схему обработки заявки в учебном центре. Она не соответствует канонам BPMN, но всё равно наглядна и понятна.

Фрагмент процессной модели бизнес-процесса: основные действия менеджера по продажам
Инфографика: Майя Мальгина для Skillbox Media

Это вариант моделирования «для себя». Его используют, чтобы структурировать общие представления о бизнес-процессе, но не раскладывать его на этапы и не составлять алгоритмов.

При ментальном подходе на процесс смотрят не как на последовательность результатов или действий, а как на набор связанных друг с другом понятий. Обычно их собирают на интеллект-карте: в центре «чёрный ящик» с процессом, на орбите — связанные с ним идеи и элементы. Жёстких рамок и нотаций нет — карты рисуют в произвольной форме.

Такая визуализация помогает найти решение, как сделать процесс эффективнее. Дальше это решение воплощают на основе процессного подхода: забирают в основную модель главные элементы, а ненужные отбрасывают.

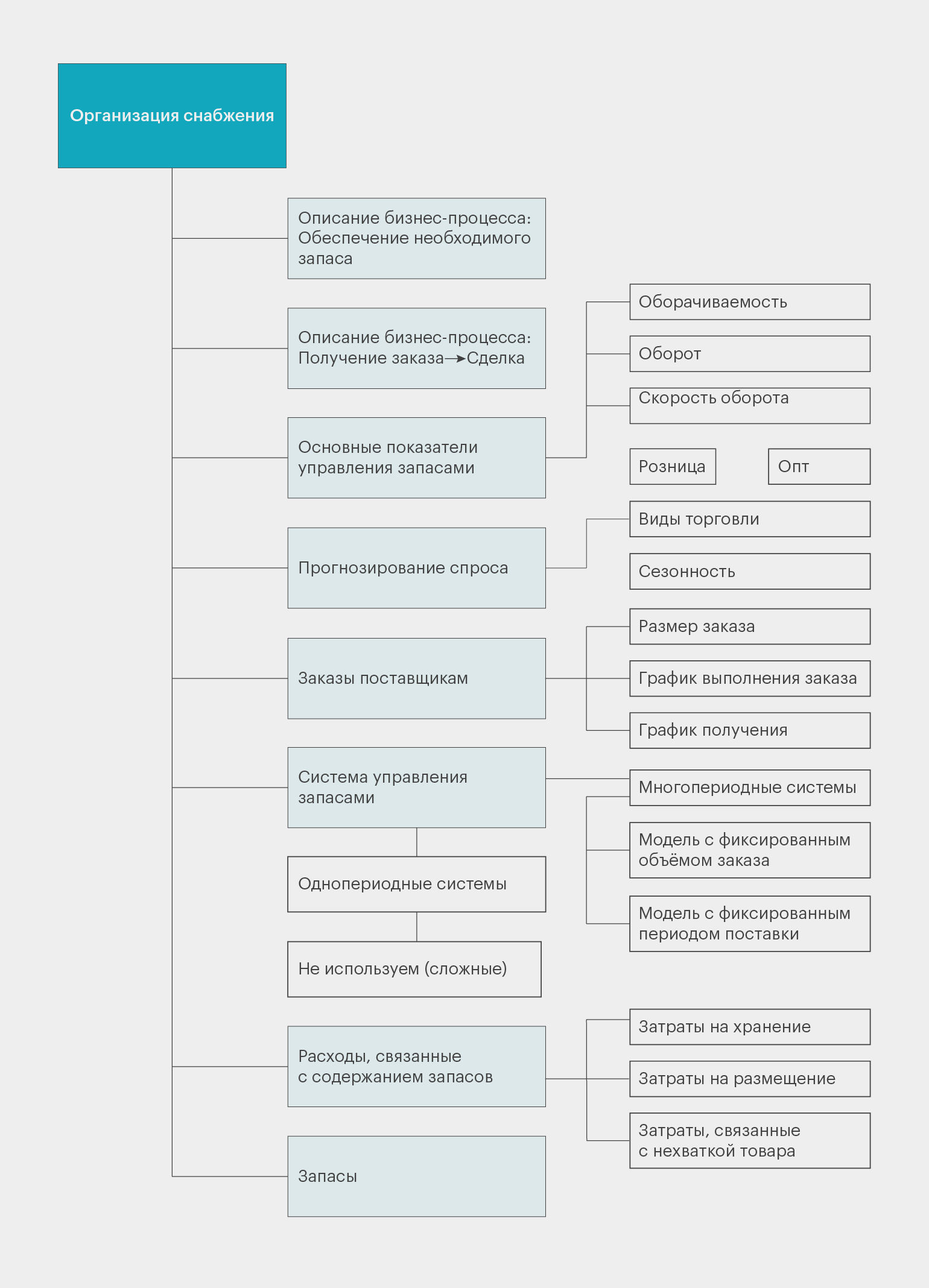
Ниже дан пример ментальной карты процесса снабжения предприятия. На карте собраны понятия, которые связаны между собой внутри процесса. Но по этапам они не распределены.

Фрагмент ментальной модели. Составлен в свободной форме — все элементы вращаются на орбите процесса
Инфографика: Майя Мальгина для Skillbox Media

Обычно моделированием бизнес-процессов занимаются внутренние сотрудники компании или подрядчики. Выбор исполнителя зависит от размеров бизнеса и целей моделирования.

Например, если нужно построить воронку продаж для CRM и при этом нет цели улучшать процессы, можно строить модель можно своими силами. Когда цель моделирования в том, чтобы оптимизировать процессы, лучше обратиться к аналитикам. Для оптимизации нужно глубоко разобраться в процессах и ещё и думать над тем, как их доработать. Потребуется опыт и знание инструментов.

Рассмотрим, кто может заниматься моделированием процессов.

Собственник и сотрудники. В небольших компаниях лучше, чтобы процессы моделировал собственник: он знает свой бизнес и сможет подробно его описать. Самих процессов в таких компаниях немного, а сложная детализация обычно не нужна.

В компаниях покрупнее собственнику лучше привлекать к моделированию помощников: собрать команду из руководителей отделов и проработать основные процессы вместе. Например, процессы в отделе продаж лучше разбирать со старшим менеджером, а процессы в цехе — с главным инженером.

Подрядчики. В среднем и крупном бизнесе моделировать бизнес-процессы внутренними силами точно не получится — количество и объём всех процессов уже не укладываются в голове собственника.

В этом случае моделированием занимается экспертная группа. В неё входят приглашённые бизнес-аналитики и специалисты, участвующие в моделируемых процессах.

Моделирование как отдельную услугу заказывают редко. Чаще это один из этапов внедрения систем автоматизации — CRM, ECM или ERP. Это работает по такой схеме:

Команда внедрения — подрядчик — приходит на территорию заказчика.
Она описывает процессы, проводит аудит и составляет аналитический отчёт с вариантами оптимизации.
Заказчик утверждает отчёт.
Подрядчик внедряет систему автоматизации с уже оптимизированными процессами.

Фрагмент отчёта бизнес-аналитика
Изображение: личный архив Александра Завьялова

Чаще всего бизнес-процессы моделируют графически, в виде карт и схем, как мы показывали выше. Иногда описывают текстом — в виде пошаговой инструкции с уточнениями, кто и что делает. Также используют таблицы: в строках пишут действия, а в столбцах — исполнителей и этапы.

На мой взгляд, графическое моделирование — наиболее удобное и наглядное. Изобразить бизнес-процессы можно двумя способами: в специальных программах для моделирования и в обычных графических редакторах.

В специальных программах. Это способ для профессионалов в моделировании.

Специальный софт удобен тем, что шаблоны нотаций уже вшиты в него, — не нужно изучать правила иллюстрирования дополнительно. Но придётся разбираться в функциональности программ.

Вот четыре конструктора, которые я использовал в своей практике для моделирования процессов:

Microsoft Visio 2010 — векторный графический редактор для создания разных видов схем: блок-схем, схем технологических процессов, моделей бизнес-процессов, планов зданий и этажей, трёхмерных карт и так далее. Платный.
Bizagi Process Modeler — программа для моделирования процессов по нотации BPMN с возможностью совместной работы. Бесплатная.
ARIS Express — программа для моделирования бизнес-процессов и оргструктуры с нотациями eEPC или BPMN. Бесплатная.
Business Studio — система, в которой можно описать, оптимизировать и регламентировать бизнес-процессы предприятия. Платная.

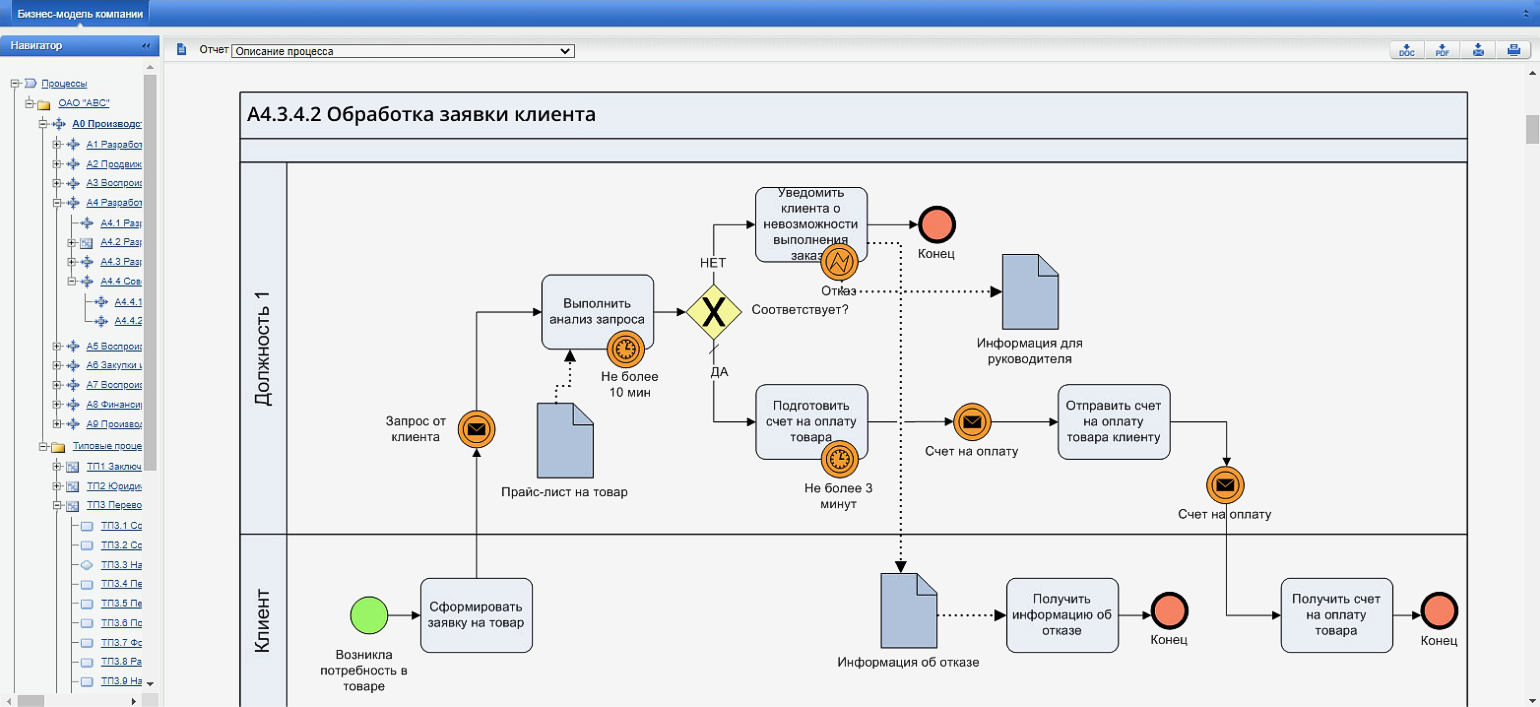
Фрагмент бизнес-модели с процессом обработки заявки в Business Studio
Скриншот: личный архив Александра Завьялова

Как правило, у всех платных конструкторов есть демоверсии, которых хватает, чтобы смоделировать простой процесс. Но повторюсь, специальное ПО — вариант для профессионалов. Не нужно тратить на него время, если вы не планируете моделировать бизнес-процессы постоянно.

В графических редакторах. Этот способ подойдёт для новичков, которые только знакомятся с моделированием бизнес-процессов. Проще всего взять обычный графический редактор — например, Microsoft Paint, Figma или Adobe Photoshop — и самостоятельно нарисовать интуитивно понятную схему процесса.

Также для изображения бизнес-процессов используют сервисы для создания ментальных карт. На мой взгляд, самые удачные из них — XMind, Diagrams и MindManager.

При выборе сервиса главное, чтобы пользователю было удобно пользоваться им и чтобы было понятно, что получается в итоге. Стандартизация и каноны при этом не так важны. На первых порах для внутреннего использования этот вариант самый доступный.

Покажем, как описать и смоделировать бизнес-процесс, на примере обработки заявки учебного центра. Использовать конструкторы не будем — все модели из примера построим в графическом редакторе.

1. Задаём точки входа и выхода. Вход — первое событие в процессе, выход — результат. Так обозначают границы, чтобы потом наполнить процесс действиями. Нужно определить:

Когда начинается процесс. В нашем примере это момент получения заявки от клиента. Если компания использует CRM, точкой входа будет попадание заявки в систему.
Когда процесс закончится. Это момент успешной реализации сделки: клиент оплатил счёт, а продавец и логист организовали доставку.

Можно придумать несколько вариантов точек входа и выхода — для разных вариантов развития события.

Задаём границы бизнес-процесса
Инфографика: Майя Мальгина для Skillbox Media

2. Описываем элементы. При составлении схемы перед глазами нужно держать основную информацию о процессе, чтобы ничего не забыть. Для этого в любом файле подробно описываем:

зачем нужен процесс;
из каких шагов и действий он состоит;
кто исполнители;
есть ли ограничения по срокам — сколько времени должен занимать весь процесс и его отдельные шаги;
какие события сопровождают действия исполнителей — например, обмен документами, информацией, денежные переводы;
какого результата нужно достичь — например, нужны подготовленные документы или оплата по счёту;
перечень ресурсов — что исполнителю нужно для реализации процесса;
показатели эффективности — по каким параметрам отслеживать, достигнута цель процесса или нет;
детали и особенности отдельных этапов.

Здесь лежит шаблон текстового описания процесса.

3. Выделяем основные этапы процесса. На основе описанного в предыдущем пункте процесса составляем блок-схему. В графическом редакторе рисуем каркас — основные этапы в пределах границ входа и выхода.

Рисуем каркас — основные этапы процесса
Инфографика: Майя Мальгина для Skillbox Media

4. Добавляем детали. Наполняем каркас «мясом» — основными событиями по процессу и действиями исполнителя по алгоритму.

Добавляем детали — основные события процесса и действия исполнителя
Инфографика: Майя Мальгина для Skillbox Media

5. Задаём роли. В процессе может быть несколько исполнительских ролей. Их может выполнять один или несколько сотрудников. Обычно роли обезличены, без уточнения фамилий, — только должности.

6. Наполняем схему ресурсами. Отмечаем на схеме источники ресурсов, которые будут использовать в бизнес-процессе. Например, какие документы кто кому и на каком этапе отправит, какие базы и системы для этого будет использовать.

В нашей «ручной» схеме — это просто дополнительные элементы в алгоритме. Если для моделирования используется специальный софт, к схеме можно прикрепить ссылки.

Блок-схема готова. Если таких схем несколько, их процессы можно связать друг с другом на одной карте.

Схемы и алгоритмы нужны, чтобы сделать процессы эффективнее и полезнее для бизнеса. Кроме этого, с готовыми моделями бизнес-процессов проще проводить автоматизацию. Об автоматизации бизнес-процессов расскажем в следующей статье.

Бизнес-процессы — любые операции внутри компании, которые помогают решать бизнес-задачи и зарабатывать. Моделирование бизнес-процессов — описание существующих в компании процессов и документирование требований к ним.
В моделировании бизнес-процессов есть три основных подхода: функциональный, процессный и ментальный. Самый понятный подход для неподготовленного человека — процессный. Он даёт подробный алгоритм действий для сотрудников и глубокую детализацию операций.
Моделировать процессы можно своими силами — если бизнес небольшой и несложный. Если в дальнейшем нужно оптимизировать процессы, лучше привлечь консультантов.
Бизнес-процессы обычно описывают графически — в виде карт и интуитивно понятных схем. Так с ними проще работать.
Смоделировать процесс можно самому: разобрать внутреннюю кухню компании, описать в тексте все алгоритмы и на основе этого построить схему в графическом редакторе.

Другие материалы Skillbox Media для менеджеров

Эффективный руководитель

Вы научитесь разрабатывать стратегию, ставить цели, создавать бизнес‑процессы и комфортный климат в команде. Найдёте точки роста в своей компании, сможете претендовать на повышение или масштабировать бизнес.

Узнать про курс

Учись бесплатно:
вебинары по программированию, маркетингу и дизайну.

Участвовать

Источник

Черемных Мариана Федоровна учитель математики и информатики МБОУ «СОШ № 1» Иркутская область г. Усть-Илимск

I этап. Постановка задачи

Описание задачи Цель моделирования
Описание задачи
Цель моделирования

II этап. Разработка модели

Информационная модель
Информационная модель

Компьютерная модель
Компьютерная модель

III этап. Компьютерный эксперимент

План эксперимента
План эксперимента

Проведение исследования
Проведение исследования

IV этап. Анализ результатов

моделирования

Результаты соответствуют цели

Результаты не соответствуют цели

По характеру постановки все задачи можно разделить на три группы:

К первой группе можно отнести задачи, в которых требуется исследовать, как изменятся характеристики объекта при некотором воздействии на него: « что будет, если?.. ».

Например, будет ли сладко, если в чай положить две чайные ложки сахара?

Вторая группа задач имеет такую формулировку: какое надо произвести воздействие на объект, чтобы его параметры удовлетворяли некоторому заданному условию? Такая постановка задачи часто называется « как сделать, чтобы?.. ».

Например, какого объема должен быть воздушный шар, наполненный гелием, чтобы он мог подняться вверх с грузом 100 кг?

Третья группа – это комплексные задачи.

Примером такого комплексного подхода может служить решение задачи о получении химического раствора заданной концентрации.

Данный этап характеризуется двумя основными моментами:

описание задачи;

определение целей моделирования;

1. Описание задачи

При описании задачи создается описательная модель с использованием естественных языков и рисунков.

Хорошо поставленной задачей является та, в которой:

описаны все связи между исходными данными и результатом; известны все исходные данные; решение существует; задача имеет единственное решение.
описаны все связи между исходными данными и результатом;
известны все исходные данные;
решение существует;
задача имеет единственное решение.

Примеры плохо поставленных задач:

Найти максимальное значение функции —
Найти максимальное значение функции —

(задача не имеет решений).

(задача не имеет решений).

Найти функцию, которая проходит через точки (0,1) и (1,0) — (множество решений).
Найти функцию, которая проходит через точки (0,1) и (1,0) — (множество решений).

2. Определение цели моделирования

Определение цели моделирования позволяет четко установить, какие исходные данные являются важными, какие — несущественны и что требуется получить на выходе.

1. Информационная модель

выбрать тип информационной модели

построить формализованную модель это модель, записанная на формальном языке, например, с помощью математического языка алгебраических формул, уравнений или неравенств. Кроме того, в соответствии с поставленной целью необходимо выделить параметры, которые известны ( исходные данные ) и которые следует найти ( результаты ), с учетом ограничений на допустимые значения этих свойств.
разработать алгоритм работы модели алгоритм – это четко определенный порядок действий, которые нужно выполнить для решения задачи.

2. Компьютерная модель

Следующий шаг – это преобразование информационной модели в компьютерную модель , т.е. выразить ее на понятном для компьютера языке. Существуют различные пути построения компьютерных моделей, в том числе:

создание компьютерной модели в форме проекта на одном из языков программирования;
построения компьютерной модели с использованием электронных таблиц, систем компьютерного черчения или других приложений. От выбора программной среды зависит алгоритм построения компьютерной модели, а также форма его представления.

Эксперимент – это исследование модели в заданных условиях.

1. Тестирование компьютерной модели

Тестирование – это проверка модели на исходных данных с известным результатом.

Для проверки правильности алгоритма построения модели используется тестовый набор исходных данных, для которых конечный результат заранее известен.

Например, если вы используете при моделировании расчетные формулы, то надо подобрать несколько вариантов исходных данных и просчитать их «вручную». Когда модель построена, вы проводите тестирование с теми же исходными данными и сравниваете результаты моделирования с расчетными данными. Если результаты совпадают, то алгоритм верный, если нет — надо устранять ошибки.

2. Исследование компьютерной модели

Если алгоритм построенной модели верный, то можно перейти ко второму пункту компьютерного эксперимента – проведение исследования компьютерной модели.

При проведении исследования, если компьютерная модель существует в виде проекта на одном из языков программирования, ее нужно запустить на выполнение, ввести исходные данные и получить результаты.

Если компьютерная модель исследуется, например, в электронных таблицах, то можно построить диаграмму или график.

Конечная цель моделирования – это анализ полученных результатов.

Основой выработки решения служат результаты тестирования и экспериментов.

Если задача решена верно, то исследования можно закончить.
Если результаты не соответствуют целям поставленной задачи, значит, на предыдущих этапах были допущены ошибки или неточности. Возможные выводы:

необходимо изменить алгоритм или условия моделирования необходимо изменить постановку задачи исправить ошибки в формулах
необходимо изменить алгоритм или условия моделирования
необходимо изменить постановку задачи
исправить ошибки в формулах

Если ошибки выявлены, то требуется корректировка модели , то есть возврат к одному из предыдущих этапов. Процесс повторяется до тех пор, пока результаты эксперимента не будут отвечать целям моделирования.

Если ошибки выявлены, то требуется корректировка модели , то есть возврат к одному из предыдущих этапов. Процесс повторяется до тех пор, пока результаты эксперимента не будут отвечать целям моделирования.

Рассмотрим задачи, на примере которых проследим этапы моделирования.

Описание задачи

Набрать и подготовить к печати текст.

Эта задача относится к постановке «что будет, если?..».

Цель : получить грамотный, отформатированный документ.

Формализация задачи

Что моделируется? — Объект «текст»
Где взять содержание текста? — имеется в виде черновика

Каков тип печати? — черно-белая
Каковы параметры текста? — абзацный отступ, границы, гарнитура, размер и начертание шрифта, цвет (черный)

Что надо получить? — набранный, отредактированный и оформленный текст

Набор текста. Информационная модель

Объект моделирования

Параметры

Текст

Название

Гарнитура шрифта

Размер

Начертания

Абзацный отступ

Выравнивание

Значения (исходные)

Ariel

Обычный

0,5 см

По ширине

Компьютерная модель

Для моделирования текстовых документов используется среда текстового процессора Word .

Сделайте коробку наибольшего объема из квадратного листа картона.

Рассмотрим этапы решения поставленной задачи.

Описание задачи

Имеется квадратный лист картона со стороной а . Из листа делают коробку следующим образом: по углам вырезают четыре квадрата и склеивают коробку по сторонам вырезов.

Цель моделирования

Определить, какова должна быть сторона вырезаемого квадрата, чтобы коробка имела наибольший объем.

Анализ объекта

В задаче рассматривается процесс преобразования одного объекта (картонного листа) в другой (коробку). Исходный объект – картонный лист – имеет заданные геометрические размеры: длина стороны а . Созданный объект – коробка – характеризуется объемом, а вырезы – размером стороны и площадью.

b см

c см

а см

b см

c см

а см

a см

Информационная модель

объект “картонный лист” имеет управляемую длину выреза b .

Действия над объектом :

вырезание квадратных областей по краям;
склеивание сторон вырезов.

Объект “коробка” имеет управляемые параметры :

площадь квадрата дна S со стороной с и объем V .

Действия над объектом:

Расчет площади основания коробки и ее объема.

Геометрическая модель:

Математическая модель:

Расчетные формулы:

Длина стороны дна с через а и b : с=а-2*b

Площадь дна: S =с*с

Нам необходимо найти объем прямоугольного параллелепипеда по формуле: V= S* b или

V= с*с* b

b см

c см

a см

Откройте табличный процессор Excel , и создайте следующую таблицу:

Высота коробки в столбце В будет изменяться от 1 до 50 с шагом 1 (используйте автозаполнение);
Длина стороны квадрата в столбце А неизменна и равна 100 см;
В столбце С длину основания коробки нужно вычислять в зависимости от величины выреза по формуле с=а-2*b, которая в ячейке С4 выглядит так: = A4-2*B4
В столбце D вычислите объём коробки по формуле V=b*c*с. В ячейку D 4 формула имеет вид: =В4*С4*С4
Выполните копирование формул в столбцах С и D . Построение компьютерной модели решения задачи завершено.

Высоту коробки (величину выреза) необходимо увеличивать, чтобы для того, чтобы найти наибольший объём.

Проанализируем полученные результаты: Очевидно, что при величине выреза 17 см наибольший объём равен 74 052 куб.см .

Для более наглядного представления, выделим данные в диапазоне ячеек D4:D50 и построим график (гистограмму) зависимости объёма коробки от величины выреза .

Измените величину шага в столбце В на 0,5, т.е. запишите в ячейку В5 число 1,5 и заполните столбец.

Проанализируйте величину объема коробки.

Проанализируйте все полученные результаты и в рабочей тетради сделайте краткие выводы.

Ответьте на вопросы:

Возможно ли проведение большего количества опытов?
Является ли наш «наилучший» результат окончательным?
Можно ли признать полученный нами результат удовлетворительным и почему?

Написать краткий конспект урока и выучить.

Источник