Модель
Фридмана. Два варианта развития Вселенной
Вселенная
Фридмана—одна из космологических
моделей,
удовлетворяющих
полевым уравнениям общей теории
относительности, первая из нестационарных
моделей Вселенной. Модель Фридмана
описывает однородную изотропную
Вселенную с веществом, обладающую
положительной, нулевой или отрицательной
постоянной кривизной.
Нестационарность
Вселенной была подтверждена открытием
зависимости красного смещения галактик
от расстояния. Независимо от Фридмана,
описываемую модель позднее разрабатывали
Леметр, Робертсон и Уокер, поэтому
решение полевых уравнений Эйнштейна,
описывающее однородную изотропную
Вселенную с постоянной кривизной,
называют моделью Фридмана-Леметра-Робертсона-Уокера.
Теорию
Большого Взрыва предложили в 20-х годах
нашего века ученые Фридман и Леметр, в
сороковых годах ее дополнил и переработал
Гамов. Согласно этой теории, когда-то
давным-давно наша Вселенная представляла
собой бесконечно малый сгусток,
сверхплотный и раскаленный до немыслимых
температур. Это нестабильное образование
внезапно взорвалось, пространство
быстро расширилось, а температура
разлетающихся частиц, обладающих высокой
энергией, начала снижаться. Примерно
после первого миллиона лет атомы двух
самых легких элементов, водорода и
гелия, стали стабильными. Под действием
сил притяжения начали концентрироваться
облака материи. В результате сформировались
галактики, звезды и другие небесные
тела. Звезды старели, взрывались
сверхновые, после чего появлялись более
тяжелые элементы. Они формировали звезды
более позднего поколения, такие, как
наше Солнце.
В
1922 г. советский математик А. А. Фридман,
анализируя уравнения общей теории
относительности Эйнштейна, пришёл к
выводу, что Вселенная не может находиться
в стационарном состоянии — она должна
либо расширяться, либо пульсировать. В
дальнейшем выводы Фридмана получили
подтверждение в астрономических
наблюдениях, обнаруживших в спектрах
галактик так называемое красное смещение
спектральных линий, что соответствует
взаимному удалению этих звездных
систем.
[1, с. 44]
(1.
Зельдович Я.Б., И.Д. Новиков. Строение и
эволюция Вселенной. М.: Наука, 1989. – 736
с.)
Модели
Фридмана
Уравнения
общей теории относительности, описывающие
эволюцию Вселенной, слишком сложны,
чтобы решить их в деталях. А потому
Фридман предложил вместо этого принять
два простых допущения: (1) Вселенная
выглядит совершенно одинаково во всех
направлениях; (2) это условие справедливо
для всех ее точек. На основе общей теории
относительности и этих двух простых
предположений Фридману удалось показать,
что мы не должны ожидать от Вселенной
стационарности. На самом деле он в 1922
г. точно предсказал то, что Эдвин Хаббл
открыл несколько лет спустя.
Предположение
о том, что Вселенная выглядит одинаковой
во всех направлениях, конечно же, не
совсем отвечает реальности. Например,
звезды нашей Галактики составляют на
ночном небе отчетливо видимую светящуюся
полосу, называемую Млечным Путем. Но
если мы обратим свой взгляд
на
далекие галактики, число их, наблюдаемое
в разных направлениях, окажется примерно
одинаковым. Так что Вселенная, похоже,
сравнительно однородна во всех
направлениях, если рассматривать ее в
космических масштабах, сопоставимых с
расстояниями между галактиками.
Несмотря
на то что модель Фридмана была удачной
и оказалась соответствующей результатам
наблюдений Хаббла, она долгое время
оставалась почти неизвестной на Западе.
О ней узнали лишь после того, как в 1935
г. американский физик Говард Робертсон
и английский математик Артур Уокер
разработали сходные модели для объяснения
открытого Хабблом однородного расширения
Вселенной.
Хотя
Фридман предложил только одну модель,
на основе двух его фундаментальных
предположений можно построить три
разные модели. В
первой
из них (именно ее и сформулировал Фридман)
расширение происходит настолько
медленно, что гравитационное притяжение
между галактиками постепенно еще больше
замедляет его, а потом и останавливает.
Галактики
тогда начинают двигаться друг к другу,
и Вселенная сжимается. Расстояние между
двумя соседними галактиками сначала
возрастает от нуля до некоторого
максимума, а затем вновь уменьшается
до нуля.
Во
втором
решении скорость расширения столь
велика, что тяготение никогда не может
его остановить, хотя и несколько
замедляет. Разделение соседних галактик
в этой модели начинается с нулевого
расстояния, а затем они разбегаются с
постоянной скоростью.
Наконец,
существует третье
решение,
в котором скорость расширения Вселенной
достаточна лишь для того, чтобы
предотвратить обратное сжатие, или
коллапс. В этом случае разделение также
начинается с нуля и возрастает бесконечно.
Однако скорость разлета постоянно
уменьшается, хотя и никогда не достигает
нуля.
Замечательной
особенностью первого типа модели
Фридмана является то, что Вселенная не
бесконечна в пространстве, но пространство
не имеет границ. Гравитация в этом случае
настолько сильна, что пространство
искривляется, замыкаясь само на себя
наподобие поверхности Земли. Путешествующий
по земной поверхности в одном направлении
никогда не встречает непреодолимого
препятствия и не рискует свалиться с
«края Земли», а попросту возвращается
в исходную точку. Таково пространство
в первой модели Фридмана, но вместо
присущих земной поверхности двух
измерений оно имеет три. Четвертое
измерение — время — обладает конечной
протяженностью, но его можно уподобить
линии с двумя краями или границами,
началом и концом.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Вселенная Фридмана—одна из космологических моделей,
удовлетворяющих полевым уравнениям общей теории относительности, первая из нестационарных моделей Вселенной. Модель Фридмана описывает однородную изотропную Вселенную с веществом, обладающую положительной, нулевой или отрицательной постоянной кривизной.
Нестационарность Вселенной была подтверждена открытием зависимости красного смещения галактик от расстояния. Независимо от Фридмана, описываемую модель позднее разрабатывали Леметр, Робертсон и Уокер, поэтому решение полевых уравнений Эйнштейна, описывающее однородную изотропную Вселенную с постоянной кривизной, называют моделью Фридмана-Леметра-Робертсона-Уокера.
Теорию Большого Взрыва предложили в 20-х годах нашего века ученые Фридман и Леметр, в сороковых годах ее дополнил и переработал Гамов. Согласно этой теории, когда-то давным-давно наша Вселенная представляла собой бесконечно малый сгусток, сверхплотный и раскаленный до немыслимых температур. Это нестабильное образование внезапно взорвалось, пространство быстро расширилось, а температура разлетающихся частиц, обладающих высокой энергией, начала снижаться. Примерно после первого миллиона лет атомы двух самых легких элементов, водорода и гелия, стали стабильными. Под действием сил притяжения начали концентрироваться облака материи. В результате сформировались галактики, звезды и другие небесные тела. Звезды старели, взрывались сверхновые, после чего появлялись более тяжелые элементы. Они формировали звезды более позднего поколения, такие, как наше Солнце.
В 1922 г. советский математик А. А. Фридман, анализируя уравнения общей теории относительности Эйнштейна, пришёл к выводу, что Вселенная не может находиться в стационарном состоянии — она должна либо расширяться, либо пульсировать. В дальнейшем выводы Фридмана получили подтверждение в астрономических наблюдениях, обнаруживших в спектрах галактик так называемое красное смещение спектральных линий, что соответствует взаимному удалению этих звездных систем. [1, с. 44]
(1. Зельдович Я.Б., И.Д. Новиков. Строение и эволюция Вселенной. М.: Наука, 1989. – 736 с.)
Модели Фридмана
Уравнения общей теории относительности, описывающие эволюцию Вселенной, слишком сложны, чтобы решить их в деталях. А потому Фридман предложил вместо этого принять два простых допущения: (1) Вселенная выглядит совершенно одинаково во всех направлениях; (2) это условие справедливо для всех ее точек. На основе общей теории относительности и этих двух простых предположений Фридману удалось показать, что мы не должны ожидать от Вселенной стационарности. На самом деле он в 1922 г. точно предсказал то, что Эдвин Хаббл открыл несколько лет спустя.
Предположение о том, что Вселенная выглядит одинаковой во всех направлениях, конечно же, не совсем отвечает реальности. Например, звезды нашей Галактики составляют на ночном небе отчетливо видимую светящуюся полосу, называемую Млечным Путем. Но если мы обратим свой взгляд
на далекие галактики, число их, наблюдаемое в разных направлениях, окажется примерно одинаковым. Так что Вселенная, похоже, сравнительно однородна во всех направлениях, если рассматривать ее в космических масштабах, сопоставимых с расстояниями между галактиками.
Несмотря на то что модель Фридмана была удачной и оказалась соответствующей результатам наблюдений Хаббла, она долгое время оставалась почти неизвестной на Западе. О ней узнали лишь после того, как в 1935 г. американский физик Говард Робертсон и английский математик Артур Уокер разработали сходные модели для объяснения открытого Хабблом однородного расширения Вселенной.
Хотя Фридман предложил только одну модель, на основе двух его фундаментальных предположений можно построить три разные модели. В первой из них (именно ее и сформулировал Фридман) расширение происходит настолько медленно, что гравитационное притяжение между галактиками постепенно еще больше замедляет его, а потом и останавливает.
Галактики тогда начинают двигаться друг к другу, и Вселенная сжимается. Расстояние между двумя соседними галактиками сначала возрастает от нуля до некоторого максимума, а затем вновь уменьшается до нуля.
Во втором решении скорость расширения столь велика, что тяготение никогда не может его остановить, хотя и несколько замедляет. Разделение соседних галактик в этой модели начинается с нулевого расстояния, а затем они разбегаются с постоянной скоростью.
Наконец, существует третье решение, в котором скорость расширения Вселенной достаточна лишь для того, чтобы предотвратить обратное сжатие, или коллапс. В этом случае разделение также начинается с нуля и возрастает бесконечно. Однако скорость разлета постоянно уменьшается, хотя и никогда не достигает нуля.
Замечательной особенностью первого типа модели Фридмана является то, что Вселенная не бесконечна в пространстве, но пространство не имеет границ. Гравитация в этом случае настолько сильна, что пространство искривляется, замыкаясь само на себя наподобие поверхности Земли. Путешествующий по земной поверхности в одном направлении никогда не встречает непреодолимого препятствия и не рискует свалиться с «края Земли», а попросту возвращается в исходную точку. Таково пространство в первой модели Фридмана, но вместо присущих земной поверхности двух измерений оно имеет три. Четвертое измерение — время — обладает конечной протяженностью, но его можно уподобить линии с двумя краями или границами, началом и концом.
https://studfiles.net/preview/2968626/
| Космология |

|
| Изучаемые объекты и процессы |
|
| История Вселенной |
|
| Наблюдаемые процессы |
|
| Теоретические изыскания |
|
Вселе́нная Фри́дмана (метрика Фридмана — Леметра — Робертсона — Уокера) — одна из космологических моделей, удовлетворяющих полевым уравнениям общей теории относительности (ОТО), первая из нестационарных моделей Вселенной. Получена Александром Фридманом в 1922. Модель Фридмана описывает однородную изотропную в общем случае нестационарную Вселенную с веществом, обладающую положительной, нулевой или отрицательной постоянной кривизной. Эта работа учёного стала первым основным теоретическим развитием ОТО после работ Эйнштейна 1915—1917 гг.
Содержание
- 1 История открытия
- 2 Метрика Фридмана-Робертсона-Уокера
- 3 Основные уравнения
- 4 Объяснение закона Хаббла
- 5 Следствия
- 5.1 Определение кривизны пространства. Понятие критической плотности
- 5.2 Эволюция плотности вещества. Уравнение состояния
- 5.3 Динамика расширения
- 6 ΛCDM
- 6.1 Возраст Вселенной
- 6.1.1 Теоретическое описание
- 6.1.2 Данные наблюдений
- 6.2 Виды расстояний.
- 6.2.1 Теоретическое описание
- 6.2.2 Данные наблюдений
- 6.3 Сфера Хаббла. Горизонт частиц. Горизонт событий
- 6.1 Возраст Вселенной
- 7 См. также
- 8 Примечания
- 9 Ссылки
История открытия
Решение Фридмана было опубликовано в авторитетном физическом журнале Zeitschrift für Physik в 1922[1] и 1924 (для Вселенной с отрицательной кривизной)[2]. Решение Фридмана было вначале отрицательно воспринято Эйнштейном (который предполагал стационарность Вселенной и даже ввёл с целью обеспечения стационарности в полевые уравнения ОТО так называемый лямбда-член), однако затем он признал правоту Фридмана. Тем не менее, работы Фридмана (умершего в 1925) остались вначале незамеченными.
Нестационарность Вселенной была подтверждена открытием зависимости красного смещения галактик от расстояния (Эдвин Хаббл, 1929). Независимо от Фридмана, описываемую модель позднее разрабатывали Леметр (1927), Робертсон и Уокер (1935), поэтому решение полевых уравнений Эйнштейна, описывающее однородную изотропную Вселенную с постоянной кривизной, называют моделью Фридмана — Леметра — Робертсона — Уокера.
Эйнштейн не раз подтверждал, что начало теории расширяющейся Вселенной положил А. А. Фридман.
В творчестве А. А. Фридмана работы по теории относительности могли бы на первый взгляд показаться довольно внезапными. Ранее в основном он работал в области теоретической гидромеханики и динамической метеорологии.
Усвоение Фридманом ОТО было весьма интенсивным и в высшей степени плодотворным. Совместно с Фредериксом он взялся за капитальный труд «Основы теории относительности», в которой предполагалось изложить «достаточно строго с логической точки зрения» основы тензорного исчисления, многомерной геометрии, электродинамики, специального и общего принципа относительности.
Книга Фредерикса и Фридмана «Основы теории относительности» — это обстоятельное, подробное изложение теории относительности, основанное на весьма солидном математическом фундаменте геометрии общей линейной связности на многообразии произвольной размерности и теории групп. Исходной для авторов оказывается геометрия пространства-времени.
В 1923 г. была опубликована популярная книга Фридмана «Мир как пространство и время», посвящённая ОТО и ориентированная на довольно подготовленного читателя. В 1924 г. появилась статья Фридмана, рассматривавшая некоторые вырожденные случаи общей линейной связности, которые, в частности, обобщают перенос Вейля и, как считали авторы, «может быть, найдут применение в физике».
И, наконец, главным результатом работы Фридмана в области ОТО стала космологическая нестационарная модель, носящая теперь его имя.
По свидетельству В. А. Фока, в отношении Фридмана к теории относительности преобладал подход математика: «Фридман не раз говорил, что его дело — указать возможные решения уравнений Эйнштейна, а там пусть физики делают с этими решениями, что они хотят»[3].
Изначально, уравнения Фридмана использовали уравнения ОТО с нулевой космологической постоянной. И модели, основанные на них, безоговорочно доминировали (помимо короткого всплеска интереса к другим моделям в 1960-е гг.) вплоть до 1998 года[4].
В тот год вышли две работы, использовавшие в качестве индикаторов расстояния — сверхновые типа Ia. В них было убедительно показано, что на больших расстояниях закон Хаббла нарушается и Вселенная расширяется ускоренно, что требует наличия тёмной энергии, известные свойства которой соответствуют Λ-члену.
Современная модель, так называемая «модель ΛCDM», по-прежнему является моделью Фридмана, но уже с учётом как космологической постоянной, так и тёмной материи.
Метрика Фридмана-Робертсона-Уокера
| Вид символов Кристоффеля |
|---|

|
| Производные выражения от символов Кристоффеля |

|
Геометрия однородной изотропной Вселенной — это геометрия однородного и изотропного трёхмерного многообразия. Метрикой таких многообразий является метрика Фридмана-Робетсона-Уокера (FWT)[5]:
где χ — так называемое сопутствующие расстояние или конформное, не зависящее от времени, в отличии от масштабного фактора a, t — время в единицах скорости света, s — интервал.
,
где k принимает значение:
- k=0 для трёхмерной плоскости
- k=1 для трёхмерной сферы
- k=-1 для трёхмерной гиперсферы
x — трёхмерный радиус-вектор в квазидекартовых координатах: 
исправить
Или в тензорной записи:
где компоненты метрического тензора равны:
где 


Основные уравнения
Если же выражение для метрики подставить в уравнения ОТО для идеальной жидкости, то получим следующую систему уравнений:
| Название | СИ | Естественная система единиц |
|---|---|---|
| Уравнение энергии |
|
|
| Уравнение движения |
|
|
| Уравнение неразрывности |
|
|
Вывод уравнений движения и энергии[6]
Запишем полевые уравнения Эйнштейна в следующей форме:
,
где Rμν — тензор Риччи:
,
a Sμν записывается в терминах энергии импульса:
Т.к. в метрике Фридмана-Робертсона-Уокера все афинные связности с двумя или тремя временными индексами обнуляются, то
,
Подставим в ненулевые компоненты тензора Риччи выражения для символов Кристофеля:
,
где 
Из всех тех же соотношений для выбранной метрики:
Тогда, в точке x=0 чисто пространственный тензор Риччи равен:
Но в точке x=0 метрика это просто δij, т.е. в начале координат имеется следующее соотношение двух три-тензоров:
И в силу однородности метрики Фридмана-Робетсона-Уокера это соотношение справедливо при любом преобразовании координат, т.е. соотношение выполняется во всех точках пространства, тогда можно записать:
Компоненты тензора энергии-импульса в нашей метрике будут следующими:
Тогда:
,
После подстановки уравнения Эйнштена примут вид:
Для перехода к уравнениям с Λ-членом необходимо произвести подстановку:
И после элементарных преобразований приходим к итоговому виду.
Вывод уравнения неразрывности[7]
Уравнение неразрывности следует из условия ковариантного сохранения тензора энергии-импульса:
Полагая здесь ν=0:
Явно запишем ненулевые компоненты тензора энергии-импульса:
подставив эти значения и воспользовавшись выражениями для символов кристофеля в FWT-метрике придем к конечному виду уравнения.
где Λ — космологическая постоянная, ρ — средняя плотность Вселенной, P, p — давление, выраженная в Си и естественной системы единиц соответственно, с — скорость света.
Приведенная система уравнений допускает множество решений, в зависимости от выбранных параметров. На самом деле значение параметров фиксированы только на текущий момент и с течением времени эволюционируют, поэтому эволюцию расширения описывает совокупность решений.[5]
Объяснение закона Хаббла
Допустим есть источник, расположенный в сопутствующей системе на расстоянии r1 от наблюдателя. Приемная аппаратура наблюдателя регистрирует фазу приходящей волны. Рассмотрим два интервала времени δt1 и δt2 между точками с одной и той же фазой[5]:
С другой стороны для световой волны в принятой метрике выполняется равенство:
Проинтегрировав это уравнение получим:
Учитывая что в сопутствующих координатах r[прояснить] не зависит от времени, и малость длины волны относительно радиуса кривизны Вселенной, получим соотношение:
Если теперь его подставить в первоначальное соотношение:
Разложим a(t) в ряд Тейлора с центром в точке a(t1) и учтем члены только первого порядка:
После приведения членов и домножения на c:
Соответственно, константа Хаббла:
Следствия
Определение кривизны пространства. Понятие критической плотности
Подставив в уравнение энергии, записанного для текущего момента, выражение для постоянной Хаббла(H0), приведем его к виду:
,
где 


плотность вещества и темной энергии, отнесенная к критической, сама критическая плотность и вклад кривизны пространства соответственно. Если переписать уравнение следующим образом
,
то станет очевидно, что:
Эволюция плотности вещества. Уравнение состояния
| Стадия | Эволюция масштабного фактора |
Параметр Хаббла |
|---|---|---|
| Инфляционная |  |

|
| Радиационное доминирование p=ρ/3 |
 |

|
| Пылевая стадия p=0 |
 |

|
 -доминирование -доминированиеp=-ρ |
 |

|
Подставив в уравнение неразрывности уравнение состояния в виде
(1)
Получим его решение:
Для разных случаев эта зависимость выглядит по-разному:
Случай холодного вещества (например пыль) p = 0
Случай горячего вещества (например излучение) p = ρ/3
Случай энергии вакуума p = -ρ
Благодаря этому, влиянием Ωk на ранних этапах можно пренебречь, то есть считать Вселенную плоской (так как k=0. Одновременно, разная зависимость плотности компонентов от масштабного фактора позволяет выделить различные эпохи, когда расширение определяется только тем или иным компонентом, представленных в таблице.
Также стоить отметить, что если ввести некую квинтэссенцию из плотности темной энергии и плотности барионной и принять, что оно подчиняется выражению (1), то пограничным значением является
При превышении этого параметра расширение замедляется, при меньшем — ускоряется.
Динамика расширения
Λ < 0
Если значение космологической постоянной отрицательно, то действуют только силы притяжения и более никаких. Правая часть уравнения энергии будет неотрицательной только при конечных значениях R. Это означает, что при некотором значении Rc Вселенная начнет сжиматься при любом значении k и вне зависимости от вида уравнения состояния[8].
Λ = 0
В случае, если космологическая постоянная равна нулю, то эволюция целиком и полностью зависит от начальной плотности вещества[5]:

Если 
Λ > 0
Если Λ>0 и k≤0, то Вселенная монотонно расширяется, но в отличие от случая с Λ=0 при больших значениях R скорость расширения растёт[8]:
![Rpropto exp[(Lambda /3)^{1/2}t].](https://wikimedia.org/api/rest_v1/media/math/render/svg/ce434c9fff9e6018a4fe3558f05f19a069c55229)
При k=1 выделенным значением является 


При Λ>Λc скорость расширения убывает до какого-то момента, а потом начинает неограниченно возрастать. Если Λ незначительно превышает Λc, то на протяжении некоторого времени скорость расширения остаётся практически неизменной.
В случае Λ<Λc всё зависит от начального значения R, с которого началось расширения. В зависимости от этого значения Вселенная либо будет расширяться до какого-то размера, а потом сожмется, либо будет неограниченно расширяться.
ΛCDM
| Космологические параметры по данным WMAP и Planck | ||
|---|---|---|
| WMAP[9] | Planck[10] | |
| Возраст Вселенной t0, млрд лет | 13,75±0,13 | 13,81±0,06 |
| Постоянная Хаббла H0, (км/с)/Мпк | 71,0±2,5 | 67,4±1,4 |
| Плотность барионной материи Ωbh2 | 0,0226±0,0006 | 0,0221±0,0003 |
| Плотность тёмной материи Ωсh2 | 0,111±0,006 | 0,120±0,003 |
| Общая плотность Ωt | 1,08+0,09 -0,07 |
1,0±0,02 |
| Плотность барионной материи Ωb | 0,045±0,003 | |
| Плотность тёмной энергии ΩΛ | 0,73±0,03 | 0,69±0,02 |
| Плотность тёмной материи Ωc | 0,22±0,03 |
ΛCDM — это современная модель расширения, являющаяся моделью Фридмана, включающая в себя помимо барионной материи, темную материю и темную энергию
Возраст Вселенной
Теоретическое описание
Время с начала расширения, называемая также возрастом Вселенной[11] определяется следующим образом:
Вывод
С учетом эволюции плотности запишем общую плотность в следующем виде:
Подставив это в уравнение энергии, получим искомое выражение
исправить
Наблюдательные подтверждения сводятся к подтверждению самой модели расширения с одной стороны и предсказываемой ею моменты начала различных эпох, а с другой, чтоб возраст самых старых объектов не превышал получающийся из модели расширения возраст всей Вселенной.
Данные наблюдений
Не существует прямых измерений возраста Вселенной, все они измеряются косвенно. Все методы можно разделить на две категории[12]:
- Определение возраста на основе моделей эволюции у самых старых объектов: старых шаровых скоплений и белых карликов.
- В первом случае метод основан на факте, что звезды в шаровом скоплении все одного возраста, опираясь на теорию звёздной эволюции, строятся изохроны на диаграмме «цвет — звёздная величина», то есть кривые равного возраста для звёзд различной массы. Сопоставляя их с наблюдаемым распределением звёзд в скоплении, можно определить его возраст.
- Метод имеет ряд своих трудностей. Пытаясь их решить, разные команды, в разное время получали разные возраста для самых старых скоплений, от ~8 млрд лет[13], до ~ 25 млрд лет[14].
- Белые карлики имеют приблизительно одинаковую массу звёзд-предшественниц, а значит — и приблизительно одинаковую зависимость температуры от времени. Определив по спектру белого карлика его абсолютную звёздную величину на данный момент и зная зависимость время—светимость при остывании, можно определить возраст карлика[15]
- Однако данный подход связан как с большими техническими трудностями, — белые карлики крайне слабые объекты, — необходимо крайне чувствительные инструменты, чтоб их наблюдать. Первым и пока единственным телескопом, на котором возможно решение данной задачи является космический телескоп им. Хаббла. Возраст самого старого скопления по данным группы, работавшей с ним:
млрд лет[15], однако, результат оспаривается. Оппоненты указывают, что не были учтены дополнительные источники ошибок, их оценка
млрд лет[16].
- Ядерный метод. В его основе лежит тот факт, что разные изотопы имеют разный период полураспада. Определяя текущие концентрации различных изотопов у первичного вещества можно определить возраст элементов в неё входящих.
- Так у звезды CS31082-001, принадлежащей звёздному населению типа II, были обнаружены линии и измерены концентрации тория и урана в атмосфере. Эти два элемента имеют различный период полураспада, поэтому со временем их соотношение меняется, и если как-то оценить первоначальное соотношение обильностей, то можно определить возраст звезды. Оценить можно двояким способом: из теории r-процессов, подтверждённой как лабораторными измерениями, так и наблюдениями Солнца; или можно пересечь кривую изменения концентраций за счёт распада и кривую изменения содержания тория и урана в атмосферах молодых звёзд за счёт химической эволюции Галактики. Оба метода дали схожие результаты: 15,5±3,2[17] млрд лет получены первым способом,
[18] млрд лет — вторым.
- Так у звезды CS31082-001, принадлежащей звёздному населению типа II, были обнаружены линии и измерены концентрации тория и урана в атмосфере. Эти два элемента имеют различный период полураспада, поэтому со временем их соотношение меняется, и если как-то оценить первоначальное соотношение обильностей, то можно определить возраст звезды. Оценить можно двояким способом: из теории r-процессов, подтверждённой как лабораторными измерениями, так и наблюдениями Солнца; или можно пересечь кривую изменения концентраций за счёт распада и кривую изменения содержания тория и урана в атмосферах молодых звёзд за счёт химической эволюции Галактики. Оба метода дали схожие результаты: 15,5±3,2[17] млрд лет получены первым способом,
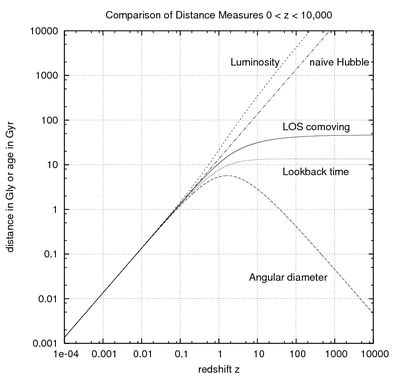
Виды расстояний.
Сравнение кривых для различных видов расстояний
Теоретическое описание
В космологии на больших расстояниях непосредственно измеряемых величин всего три — звездная величина, характеризующая блеск, угловой размер и красное смещение. Поэтому, для сравнения с наблюдениями вводятся две зависимости:
- Угловой размер от красного смещения, называемого угловым расстоянием:
Вывод
По определению:
D — собственный размер объекта перпендикулярно к лучу зрения, Δθ — видимый угловой размер.
Рассмотрим метрику в сферических координатах:
Размер объекта много меньше расстояния до него, поэтому:
.
Вследствие малости углового размера dΩ можно принять равным Δθ. Перейдя в метрику текущего момента времени получим конечное выражение
- Блеск от красного смещения — называемого фотометрическим расстоянием:
Вывод
По определению:
Поток излучения от некоторого источника уменьшается из-за геометрического фактора (


После чего путём простых преобразований получаем исходный вид
Также в научно-популярной литературе можно встретить еще три вида расстояний: расстояние между объектами на текущей момент, расстояние между объектами на момент испускания принятого нами света и расстояние, которое прошел свет.
Данные наблюдений
Для измерения фотометрического расстояния необходим источник известной светимости, так называемая стандартная свеча. Для космологических масштабов в качестве таковой берутся сверхновые типа Ia. Они возникают как следствие термоядерного взрыва белого карлика приблизившегося к пределу Чандрасекара.
Сфера Хаббла. Горизонт частиц. Горизонт событий
Также преимущественно в научно-популярной литературе используется термин «сфера Хаббла» — это сфера чей радиус равен расстоянию при котором скорость убегания равна скорости света.[19][20]
См. также
- Большой взрыв
- Жорж Леметр
- Решения уравнений Эйнштейна
- Уравнение Фридмана (геофизическая гидродинамика)
- Уравнение Фридмана
- Фридман, Александр Александрович
Примечания
- ↑ Friedmann, A: Über die Krümmung des Raumes (О кривизне пространства), Z. Phys. 10 (1922) 377—386.
- ↑ Friedmann, A: Über die Möglichkeit einer Welt mit konstanter negativer Krümmung des Raumes (О возможности Вселенной с постоянной отрицательной кривизной пространства), Z. Phys. 21 (1924) 326—332.
- ↑ Фок В.А. (1963). «Работы А. А. Фридмана по теории тяготения Эйнштейна». УФН LXXX (3): 353–356. Проверено 2012-07-04.
- ↑ О непопулярности моделей с космологической постоянной красноречиво говорит тот факт, что Вайнберг в своей книге «Космология и гравитация» (на русском языке издана в 1975 году) параграф о моделях с космологической постоянной относит в раздел вместе с наивными моделями и моделями стационарной Вселенной, отводя на описание 4 страницы из 675.
- ↑ 1 2 3 4
- А.В. Засов.,К.А. Постнов. Общая Астрофизика. — Фрязино: Век 2, 2006. — С. 421-432. — 496 с. — ISBN 5-85099-169-7.
- Д.С. Горбунов, В.А. Рубаков. Введение в теорию ранней Вселенной: Теория горячего Большого взрыва.. — Москва: ЛКИ, 2008. — С. 45-80. — 552 с. — ISBN 978-5-382-00657-4.
- Стивен Вайнберг. Космология. — Москва: УРСС, 2013. — С. 21-81. — 608 с. — ISBN 978-5-453-00040-1.
- ↑ Стивен Вайнберг. Космология. — Москва: УРСС, 2013. — С. 57-59. — 608 с. — ISBN 978-5-453-00040-1.
- ↑ Д.С. Горбунов, В.А. Рубаков. Введение в теорию ранней Вселенной: Теория горячего Большого взрыва.. — Москва: ЛКИ, 2008. — С. 63. — 552 с. — ISBN 978-5-382-00657-4.
- ↑ 1 2
Майкл Роуэн-Робинсон. Космология = Cosmology / Перевод с английского Н.А. Зубченко. Под научной редакцией П.К. Силаева. — М.-Ижевск: НИЦ «Регулярная и хаотическая динамика», 2008. — С. 96-102. — 256 с. — ISBN 976-5-93972-659-7. - ↑ Jarosik, N., et.al. (WMAP Collaboration). Seven-Year Wilkinson Microwave Anisotropy Probe (WMAP) Observations: Sky Maps, Systematic Errors, and Basic Results (PDF). nasa.gov. Проверено 4 декабря 2010. Архивировано 16 августа 2012 года. (from NASA’s WMAP Documents page)
- ↑ Planck Collaboration. Planck 2013 results. XVI. Cosmological parameters. — arXiv:1303.5076.
- ↑ Астронет > Вселенная
- ↑ Donald D. Clayton. COSMOLOGY, COSMOCHRONOLOGY.
- ↑ Gratton Raffaele G., Fusi Pecci Flavio, Carretta Eugenio и др. Ages of Globular Clusters from HIPPARCOS Parallaxes of Local Subdwarfs. — Astrophysical Journal, 1997.
- ↑ Peterson Charles J. Ages of globular clusters. — Astronomical Society of the Pacific, 1987.
- ↑ 1 2 Harvey B. Richer et al. Hubble Space Telescope Observations of White Dwarfs in the Globular Cluster M4. — Astrophysical Journal Letters, 1995.
- ↑ Moehler S, Bono G. White Dwarfs in Globular Clusters. — 2008.
- ↑ Schatz Hendrik, Toenjes Ralf, Pfeiffer Bernd. Thorium and Uranium Chronometers Applied to CS 31082-001. — The Astrophysical Journal, 2002.
- ↑ N. Dauphas. URANIUM-THORIUM COSMOCHRONOLOGY. — 2005.
- ↑ Сергей Попов. Сверхсветовое разбегание галактик и горизонты Вселенной: путаница в тонкостях.
- ↑ TM Davis & CH Linewater. Expanding Confusion: common misconceptions of cosmological horizons and the superluminal expansion of the universe. — 2003. — arXiv:astro-ph/0310808.
Ссылки
https://ru.wikipedia.org/wiki/%D0%92%D1%81%D0%B5%D0%BB%D0%B5%D0%BD%D0%BD%D0%B0%D1%8F_%D0%A4%D1%80%D0%B8%D0%B4%D0%BC%D0%B0%D0%BD%D0%B0
| Космология |
|
| Изучаемые объекты и процессы |
|
| Наблюдаемые процессы |
|
| Теоретические изыскания |
|
| Родственные темы |
|
|
This box:
|
Запрос «Модель Фридмана» перенаправляется сюда; экономической модели инфляции см. Модель Фридмана (экономика).
Вселе́нная Фри́дмана (метрика Фридмана — Леметра — Робертсона — Уокера) — одна из космологических моделей, удовлетворяющих полевым уравнениям общей теории относительности (ОТО), первая из нестационарных моделей Вселенной. Получена Александром Фридманом в 1922. Модель Фридмана описывает однородную изотропную в общем случае нестационарную Вселенную с веществом, обладающую положительной, нулевой или отрицательной постоянной кривизной. Эта работа учёного стала первым основным теоретическим развитием ОТО после работ Эйнштейна 1915—1917 гг.
История открытия
Решение Фридмана было опубликовано в авторитетном физическом журнале Zeitschrift für Physik в 1922[1] и 1924 (для Вселенной с отрицательной кривизной)[2]. Решение Фридмана было вначале отрицательно воспринято Эйнштейном (который предполагал стационарность Вселенной и даже ввёл с целью обеспечения стационарности в полевые уравнения ОТО так называемый лямбда-член), однако затем он признал правоту Фридмана. Тем не менее, работы Фридмана (умершего в 1925) остались вначале незамеченными.
Нестационарность Вселенной была подтверждена открытием зависимости красного смещения галактик от расстояния (Эдвин Хаббл, 1929). Независимо от Фридмана, описываемую модель позднее разрабатывали Леметр (1927), Робертсон и Уокер (1935), поэтому решение полевых уравнений Эйнштейна, описывающее однородную изотропную Вселенную с постоянной кривизной, называют моделью Фридмана — Леметра — Робертсона — Уокера.
Эйнштейн не раз подтверждал, что начало теории расширяющейся Вселенной положил А. А. Фридман.
В творчестве А. А. Фридмана работы по теории относительности могли бы на первый взгляд показаться довольно внезапными. Ранее в основном он работал в области теоретической гидромеханики и динамической метеорологии.
Усвоение Фридманом ОТО было весьма интенсивным и в высшей степени плодотворным. Совместно с Фредериксом он взялся за капитальный труд «Основы теории относительности», в которой предполагалось изложить «достаточно строго с логической точки зрения» основы тензорного исчисления, многомерной геометрии, электродинамики, специального и общего принципа относительности.
Книга Фредерикса и Фридмана «Основы теории относительности» — это обстоятельное, подробное изложение теории относительности, основанное на весьма солидном математическом фундаменте геометрии общей линейной связности на многообразии произвольной размерности и теории групп. Исходной для авторов оказывается геометрия пространства-времени.
В 1923 г. была опубликована популярная книга Фридмана «Мир как пространство и время», посвящённая ОТО и ориентированная на довольно подготовленного читателя. В 1924 г. появилась статья Фридмана, рассматривавшая некоторые вырожденные случаи общей линейной связности, которые, в частности, обобщают перенос Вейля и, как считали авторы, «может быть, найдут применение в физике».
И, наконец, главным результатом работы Фридмана в области ОТО стала космологическая нестационарная модель, носящая теперь его имя.
По свидетельству В. А. Фока, в отношении Фридмана к теории относительности преобладал подход математика: «Фридман не раз говорил, что его дело — указать возможные решения уравнений Эйнштейна, а там пусть физики делают с этими решениями, что они хотят»[3].
Изначально, уравнения Фридмана использовали уравнения ОТО с нулевой космологической постоянной. И модели, основанные на них, безоговорочно доминировали (помимо короткого всплеска интереса к другим моделям в 1960-е гг.) вплоть до 1998 года[4].
В тот год вышли две работы, использовавшие в качестве индикаторов расстояния — сверхновые типа Ia. В них было убедительно показано, что на больших расстояниях закон Хаббла нарушается и Вселенная расширяется ускоренно, что требует наличия тёмной энергии, известные свойства которой соответствуют Λ-члену.
Современная модель, так называемая «модель ΛCDM», по прежнему является моделью Фридмана, но уже с учётом как космологической постоянной, так и тёмной материи.
Метрика Фридмана-Робертсона-Уокера
| Вид символов Кристоффеля |
|---|
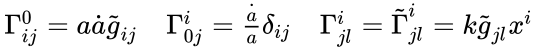
|
| Производные выражения от символов Кристоффеля |
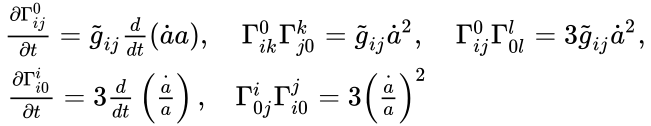
|
Геометрия однородной изотропной Вселенной — это геометрия однородного и изотропного трёхмерного многообразия. Метрикой таких многообразий является метрика Фридмана-Робетсона-Уокера (FWT)[5]:
χ — так называемое сопустствующие расстояние или конформное, не зависящее от времени, t — время в единицах скорости света.
- Шаблон:Формулы
Или в тензорной записи:
, где компоненты метрического тензора равны:
,
где 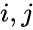
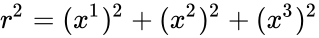
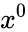
Основные уравнения
Если же выражение для метрики подставить в уравнения ОТО для идеальной жидкости, то получим следующую систему уравнений:
Вывод уравнений движения и энергии[6]
Вывод уравнения неразрывности[7]
- Уравнение энергии
- Уравнение движения
- Уравнение неразрывности
где Λ — космологическая постоянная, ρ — средняя плотность Вселенной, P — давление, с — скорость света.
Приведенная система уравнений допускает множество решений, в зависимости от выбранных параметров. На самом деле значение параметров фиксированы только на текущий момент и с течением времени эволюционируют, поэтому эволюцию расширения описывает совокупность решений.[5]
Объяснение закона Хаббла
Допустим есть источник, расположенный в сопутствующей системе на расстоянии r1 от наблюдателя. Приемная аппаратура наблюдателя регистрирует фазу приходящей волны. Рассмотрим два интервала между точками с одной и той же фазой[5]:
С другой стороны для световой волны в принятой метрике выполняется равенство:
Проинтегрировав это уравнение получим:
Учитывая что в сопутствующих координатах r не зависит от времени, и малость длины волны относительно радиуса кривизны Вселенной, получим соотношение:
Если теперь его подставить в первоначальное соотношение:
Разложим a(t) в ряд Тейлора с центром в точке a(t1) и учтем члены только первого порядка:
После приведения членов и домножения на c:
Соответственно, константа Хаббла:
Следствия
Определение кривизны пространства. Понятие критической плотности
Подставив в уравнение энергии выражение для постоянной Хаббла, приведем его к виду:
,
где
плотность вещества и темной энергии, отнесенная к критической, сама критическая плотность и вклад кривизны пространства соответственно. Если переписать уравнение следующим образом
,
то станет очевидно, что:
Эволюция плотности вещества. Уравнение состояния.
| Стадия | Эволюция 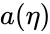 |
Параметр Хаббла |
|---|---|---|
| Инфляционная |  |
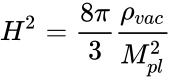
|
| Радиационное доминирование p=ρ/3 |
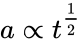 |
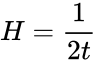
|
| Пылевая стадия p=0 |
 |
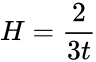
|
 -доминирование -доминированиеp=-ρ |
 |
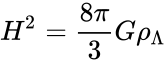
|
Подставив в уравнение неразрывности уравнение состояния в виде
(1)
Получим его решение:
Для разных случаев эта зависимость выглядит по-разному:
Случай холодного вещества (например пыль) p = 0
Случай горячего вещества (например излучение) p = ρ/3
Случай энергии вакуума p = -ρ
Благодаря этому, влиянием Ωk на ранних этапах можно пренебречь, т.е. считать Вселенную плоской (т.к. k=0. Одновременно, разная зависимость плотности компонентов от масштабного фактора позволяет выделить различные эпохи, когда расширение определяется только тем или иным компонентом, представленных в таблице.
Также стоить отметить, что если ввести некую квинтэссенция из плотностей темной энергии и плотность барионной и принять, что оно подчиняется выражению (1), то пограничным значением является
При превышении этого параметра расширение замедляется, при меньшем — ускоряется.
Динамика расширения
Λ < 0
Если значение космологической постоянной отрицательно, то действуют только силы притяжения и более никаких. Правая часть уравнения энергии будет неотрицательной только при конечных значениях R. Это означает, что при некотором значении Rc Вселенная начнет сжиматься при любом значении k и вне зависимости от вида уравнения состояния[8].
Λ = 0
В случае, если космологическая постоянная равна нулю, то эволюция при заданном значении H0 целиком и полностью зависит от начальной плотности вещества[5]:

Если 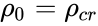
Λ > 0
Если Λ>0 и k≤0, то Вселенная монотонно расширяется, но в отличие от случая с Λ=0 при больших значениях R скорость расширения растёт[8]:
![{displaystyle Rpropto exp[(Lambda /3)^{1/2}t].}](https://wikimedia.org/api/rest_v1/media/math/render/png/ce434c9fff9e6018a4fe3558f05f19a069c55229)
При k=1 выделенным значением является 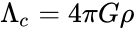
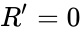
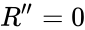
При Λ>Λc скорость расширения убывает до какого-то момента, а потом начинает неограниченно возрастать. Если Λ незначительно превышает Λc, то на протяжении некоторого времени скорость расширения остаётся практически неизменной.
В случае Λ<Λc всё зависит от начального значения R, с которого началось расширения. В зависимости от этого значения Вселенная либо будет расширяться до какого-то размера, а потом сожмется, либо будет неограниченно расширяться.
ΛCDM
| Космологические параметры по данным WMAP и Planck | ||
|---|---|---|
| WMAP[9] | Planck[10] | |
| Возраст Вселенной t0, млрд лет | 13,75±0,13 | 13,81±0,06 |
| Постоянная Хаббла H0, (км/с)/Мпк | 71,0±2,5 | 67,4±1,4 |
| Плотность барионной материи Ωbh2 | 0,0226±0,0006 | 0,0221±0,0003 |
| Плотность тёмной материи Ωсh2 | 0,111±0,006 | 0,120±0,003 |
| Общая плотность Ωt | 1,08+0,09-0,07 | 1,0±0,02 |
| Плотность барионной материи Ωb | 0,045±0,003 | |
| Плотность тёмной энергии ΩΛ | 0,73±0,03 | 0,69±0,02 |
| Плотность тёмной материи Ωc | 0,22±0,03 |
ΛCDM — это современная модель расширения, являющаяся моделью Фридмана, включающая в себя помимо барионной материи, темную материю и темную энергию
Возраст Вселенной
Теоретическое описание
Время с начала расширения, называемая также возрастом Вселенной[11] определяется следующим образом:
- Шаблон:Формулы
Наблюдательные подтверждения сводятся к подтверждению самой модели расширения с одной стороны и предсказываемой ею моменты начала различных эпох, а с другой, чтоб возраст самых старых объектов не превышал получающийся из модели расширения возраст всей Вселенной.
Данные наблюдений
Не существует прямых измерений возраста Вселенной, все они измеряются косвенно. Все методы можно разделить на две категории[12]:
- Определение возраста на основе моделей эволюции у самых старых объектов: старых шаровых скоплений и белых карликов.
- В первом случае метод основан на факте, что звезды в шаровом скоплении все одного возраста, опираясь на теорию звёздной эволюции, строятся изохроны на диаграмме «цвет — звёздная величина», то есть кривые равного возраста для звёзд различной массы. Сопоставляя их с наблюдаемым распределением звёзд в скоплении, можно определить его возраст.
- Метод имеет ряд своих трудностей. Пытаясь их решить, разные команды, в разное время получали разные возраста для самых старых скоплений, от ~8 млрд лет[13], до ~ 25 млрд лет[14].
- Белые карлики имеют приблизительно одинаковую массу звёзд-предшественниц, а значит — и приблизительно одинаковую зависимость температуры от времени. Определив по спектру белого карлика его абсолютную звёздную величину на данный момент и зная зависимость время—светимость при остывании, можно определить возраст карлика[15]
- Однако данный подход связан как с большими техническими трудностями, — белые карлики крайне слабые объекты, — необходимо крайне чувствительные инструменты, чтоб их наблюдать. Первым и пока единственным телескопом, на котором возможно решение данной задачи является космический телескоп им. Хаббла. Возраст самого старого скопления по данным группы, работавшей с ним:
млрд лет[15], однако, результат оспаривается. Оппоненты указывают, что не были учтены дополнительные источники ошибок, их оценка
млрд лет[16].
- Ядерный метод. В его основе лежит тот факт, что разные изотопы имеют разный период полураспада. Определяя текущие концентрации различных изотопов у первичного вещества можно определить возраст элементов в нее входящих.
- Так у звезды CS31082-001, принадлежащей звёздному населению типа II, были обнаружены линии и измерены концентрации в атмосфере тория и урана. Эти два элемента имеют различный период полураспада, поэтому со временем их соотношение меняется, и если как-то оценить первоначальное соотношение обильностей, то можно определить возраст звезды. Оценить можно двояким способом: из теории r-процессов, подтверждённой как лабораторными измерениями, так и наблюдениями Солнца; или можно пересечь кривую изменения концентраций за счёт распада и кривую изменения содержания тория и урана в атмосферах молодых звёзд за счёт химической эволюции Галактики. Оба метода дали схожие результаты: 15,5±3,2[17] млрд лет получены первым способом,
[18] млрд лет — вторым.
- Так у звезды CS31082-001, принадлежащей звёздному населению типа II, были обнаружены линии и измерены концентрации в атмосфере тория и урана. Эти два элемента имеют различный период полураспада, поэтому со временем их соотношение меняется, и если как-то оценить первоначальное соотношение обильностей, то можно определить возраст звезды. Оценить можно двояким способом: из теории r-процессов, подтверждённой как лабораторными измерениями, так и наблюдениями Солнца; или можно пересечь кривую изменения концентраций за счёт распада и кривую изменения содержания тория и урана в атмосферах молодых звёзд за счёт химической эволюции Галактики. Оба метода дали схожие результаты: 15,5±3,2[17] млрд лет получены первым способом,
Виды расстояний.
Файл:CosmoDistanceMeasures z to 1e4.png Сравнение кривых для различных видов расстояний
Теоретическое описание
В космологии на больших расстояниях непосредственно измеряемых величин всего три — звездная величина, характеризующая блеск, угловой размер и красное смещение. Поэтому, для сравнения с наблюдениями вводятся две зависимости:
- Угловой размер от красного смещения, называемого угловым расстоянием:
- Блеск от красного смещения — называемого фотометрическим расстоянием:
Также в научно-популярной литературе можно встретить еще три вида расстояний: расстояние между объектами на текущей момент, расстояние между объектами на момент испускания принятого нами света и расстояние, которое прошел свет.
Данные наблюдений
-
Подробнее см. также: Шкала расстояний
Для измерения фотометрического расстояния необходим источник известной светимости, так называемая стандартная свеча. Для космологических масштабов в качестве таковой берутся сверхновые типа Ia. Они возникают как следствие термоядерного взрыва белого карлика приблизившегося к пределу Чандрасекара.
Сфера Хаббла. Горизонт частиц. Горизонт событий
Также преимущественно в научно-популярной литературе используется термин «сфера Хаббла» — это сфера чей радиус равен расстоянию при котором скорость убегания равна скорости света.[19][20]
См. также
- Уравнение Фридмана
Примечания
- ↑ Friedmann, A: Über die Krümmung des Raumes (О кривизне пространства), Z. Phys. 10 (1922) 377—386.
- ↑ Friedmann, A: Über die Möglichkeit einer Welt mit konstanter negativer Krümmung des Raumes (О возможности Вселенной с постоянной отрицательной кривизной пространства), Z. Phys. 21 (1924) 326—332.
- ↑ Фок В.А. (1963). «Работы А. А. Фридмана по теории тяготения Эйнштейна». УФН LXXX (3): 353–356. Retrieved on 2012-07-04.
- ↑ О непопулярности моделей с космологической постоянной красноречиво говорит тот факт, что Вайнберг в своей книге «Космология и гравитация» (на русском языке издана в 1975 году) параграф о моделях с космологической постоянной относит в раздел вместе с наивными моделями и моделями стационарной Вселенной, отводя на описание 4 страницы из 675.
- ↑ 5,0 5,1 5,2 5,3
- А.В. Засов.,К.А. Постнов. Общая Астрофизика. — Фрязино: Век 2, 2006. — С. 421-432. — 496 с. — ISBN 5-85099-169-7. (см. ISBN )
- Д.С. Горбунов, В.А. Рубаков. Введение в теорию ранней Вселенной: Теория горячего Большого взрыва.. — Москва: ЛКИ, 2008. — С. 45-80. — 552 с. — ISBN 978-5-382-00657-4. (см. ISBN )
- Стивен Вайнберг. Космология. — Москва: УРСС, 2013. — С. 21-81. — 608 с. — ISBN 978-5-453-00040-1. (см. ISBN )
- ↑ Стивен Вайнберг. Космология. — Москва: УРСС, 2013. — С. 57-59. — 608 с. — ISBN 978-5-453-00040-1. (см. ISBN )
- ↑ Д.С. Горбунов, В.А. Рубаков. Введение в теорию ранней Вселенной: Теория горячего Большого взрыва.. — Москва: ЛКИ, 2008. — С. 63. — 552 с. — ISBN 978-5-382-00657-4. (см. ISBN )
- ↑ 8,0 8,1
Майкл Роуэн-Робинсон. Космология = Cosmology / Перевод с английского Н.А. Зубченко. Под научной редакцией П.К. Силаева. — М.-Ижевск: НИЦ «Регулярная и хаотическая динамика», 2008. — С. 96-102. — 256 с. — ISBN 976-5-93972-659-7. (см. ISBN )
- ↑ Jarosik, N., et.al. (WMAP Collaboration). Seven-Year Wilkinson Microwave Anisotropy Probe (WMAP) Observations: Sky Maps, Systematic Errors, and Basic Results (PDF). nasa.gov. Проверено 4 декабря 2010. Архивировано из первоисточника 16 августа 2012. (from NASA’s WMAP Documents page)
- ↑ Planck Collaboration Planck 2013 results. XVI. Cosmological parameters.
- ↑ Астронет > Вселенная
- ↑ Donald D. Clayton. COSMOLOGY, COSMOCHRONOLOGY.
- ↑ Gratton Raffaele G., Fusi Pecci Flavio, Carretta Eugenio и др Ages of Globular Clusters from HIPPARCOS Parallaxes of Local Subdwarfs. — 1997.
- ↑ Peterson Charles J. Ages of globular clusters. — 1987.
- ↑ 15,0 15,1 Harvey B. Richer et al. Hubble Space Telescope Observations of White Dwarfs in the Globular Cluster M4. — 1995.
- ↑ Moehler S, Bono G. White Dwarfs in Globular Clusters. — 2008.
- ↑ Schatz Hendrik, Toenjes Ralf, Pfeiffer Bernd Thorium and Uranium Chronometers Applied to CS 31082-001. — 2002.
- ↑ N. Dauphas URANIUM-THORIUM COSMOCHRONOLOGY. — 2005.
- ↑ Сергей Попов. Сверхсветовое разбегание галактик и горизонты Вселенной: путаница в тонкостях.
- ↑ TM Davis & CH Linewater Expanding Confusion: common misconceptions of cosmological horizons and the superluminal expansion of the universe. — 2003.
Ссылки
|
Выделить Вселенная Фридмана и найти в:
|
|
|
- Страница 0 — краткая статья
- Страница 1 — энциклопедическая статья
- Разное — на страницах: 2 , 3 , 4 , 5
- Прошу вносить вашу информацию в «Вселенная Фридмана 1», чтобы сохранить ее
Комментарии читателей:
Содержание (план)
1.1. Пространство-время
2.1. Расширение Вселенной
В 20-х гг. XX столетия выдающийся советский физик А. А. Фридман установил, что из уравнений общей теории относительности следует, что Вселенная не может быть неизменной, она должна эволюционировать. Наш мир должен сжиматься или расширяться. С точки зрения наблюдателя (независимо от того, в какой точке он находится: ведь мир однороден и в каждой точке все происходит так же, как и во всех остальных), все далёкие объекты удаляются от него (или приближаются к нему) с тем большей скоростью, чем дальше они расположены. При этом изменяется средняя плотность вещества во Вселенной. В наблюдениях расширение Вселенной проявляется в том, что в спектрах далёких галактик линии поглощения смещаются в красную сторону спектра. Это называется красным смещением.
Красное смещение легко снимает фотометрический парадокс. Ведь при переходе ко все более и более удалённым объектам яркость звезды уменьшается ещё и потому, что из-за красного смещения уменьшается энергия кванта. Когда скорость удаления приближается к скорости света, звезда становится невидимой.
Критическая плотность Вселенной
В теории Фридмана появляется величина, называемая критической плотностью; она может быть выражена через постоянную Хаббла:
ρк = 3H2 / 8πG,
где H — постоянная Хаббла; G — гравитационная постоянная.
Пространство-время
В больших масштабах (десятки и сотни мегапарсек) свойства пространства и времени зависят от средней плотности вещества во Вселенной (ρ̅).
Если эта плотность меньше критического значения (ρ̅к), то мир бесконечен во времени и пространстве. Его геометрические свойства описываются геометрией Лобачевского, в которой предполагается, что через точку можно провести любое количество прямых, параллельных данной.
При ρ̅=ρк мир описывается привычной нам геометрией Евклида (через точку можно провести только одну прямую, параллельную данной). В этих случаях мир бесконечен.
При ρ̅>ρк мир имеет конечный объем и в нем содержится конечная масса вещества. При этом мир не имеет границ. Представить себе такой мир невозможно, ибо мы ощущаем только трёхмерный мир. В общей теории относительности мир четырёхмерный: три пространственных измерения и время. Ближайшим, привычным нам аналогом замкнутого, конечного мира является поверхность шара. Она тоже конечна и не имеет границ.
Средняя плотность Вселенной
В настоящее время не совсем ясно какова в действительности средняя плотность во Вселенной. По современным оценкам значение средней плотности лежит между 5 • 10-27 и 3 • 10-28 кг/см3. Но эти оценки основаны на наблюдаемых формах материи и в несколько раз меньше критической. По общему мнению, средняя плотность практически совпадает с критической.
Расширение Вселенной
Дальнейшая «судьба» Вселенной зависит от её средней плотности (ρ̅). Если ρ̅>ρк, то скорость расширения будет замедляться, в конце концов расширение сменится сжатием и Вселенная вернётся к исходному состоянию. Если ρ≤ρк, то расширение будет происходить неограниченно долго. Материал с сайта http://wikiwhat.ru
Космологическая сингулярность
Общая теория относительности позволяет интерпретировать постоянную Хаббла как величину, обратную промежутку времени, прошедшего с момента возникновения Вселенной:
H = 1 / T.
Действительно, если идти по шкале времени назад, то получается, что примерно 15—20 млрд лет Вселенная имела нулевые размеры и бесконечную плотность. Такое состояние принято называть сингулярностью. Она появляется во всех вариантах фридмановской модели. Ясно, что здесь лежит предел применимости теории и нужно выходить за рамки этой модели. При достаточно малых временах квантовые эффекты (ОТО чисто классическая теория) становятся определяющими.
На этой странице материал по темам:
-
А.а фридман модель расширяющейся вселенной
-
Вселенная будет расширяться вечно, если средняя плотность вселенной
-
Плотность вселенной равна
-
Космологическая модель вселенной фридмана очень кратко
-
Геометрия евклида при критической плотности
Сто тридцать один год назад родился гениальный русский космолог Александр Фридман
«Воды, в которые я вступаю, не пересекал еще никто»
Александр Фридман
В 1922 году физик из Петрограда Александр Фридман открывает, что уравнения общей теории относительности Эйнштейна допускают не только статические, но и динамические решения.
Суть этих работ известный российско-американский историк науки Алексей Кожевников описал в докладе «Культурная среда теории Большого взрыва: пространство–время, смерть–воскрешение и Русская революция», который он прочитал в Институте гуманитарных историко-теоретических исследований имени А. В. Полетаева (ИГИТИ) ВШЭ (полную версию доклада «Стимул» предполагает опубликовать на следующей неделе):.
«Фридман предложил рассматривать вселенную как вселенную с меняющимся радиусом. Непонятно зачем, потому что никто тогда не хотел жить в такой вселенной. Все хотели бы жить в стабильной, как шарик, вселенной. Именно такую модель предложил Эйнштейн в 1917 году. В рамках релятивистской космологии Эйнштейном были предложены две стационарные модели вселенной, и физики обсуждали, какая из них лучше. А Фридман решил исследовать предположение — что будет, если радиус вселенной будет меняться? Дальше в игру уже вступала математика. Фридман утверждал, что можно найти три класса решений с таким качественным развитием. В каждом из таких классов бесконечное число решений. В стационарной модели Эйнштейна это модель типа шарика, было бесконечное число решений: для каждого радиуса можно было указать свое решение. А решения определялись двумя параметрами, каждый из которых мог иметь любое значение — радиус вселенной и ее плотность. Решение давало возможность понять, в зависимости от выбранных параметров, в какой примерно точке мы находимся, и понять, что будет со вселенной дальше.
Почему Фридману захотелось рассматривать вселенную с меняющимся радиусом, он не объяснил, но выводит все математические следствия этой гипотезы. Эту гипотезу поначалу практически все отвергли, включая самого Эйнштейна. Потребовались десятилетия, когда стали появляться эмпирические данные, чтобы к ней вернуться, когда уже другие люди тоже стали ее поддерживать».
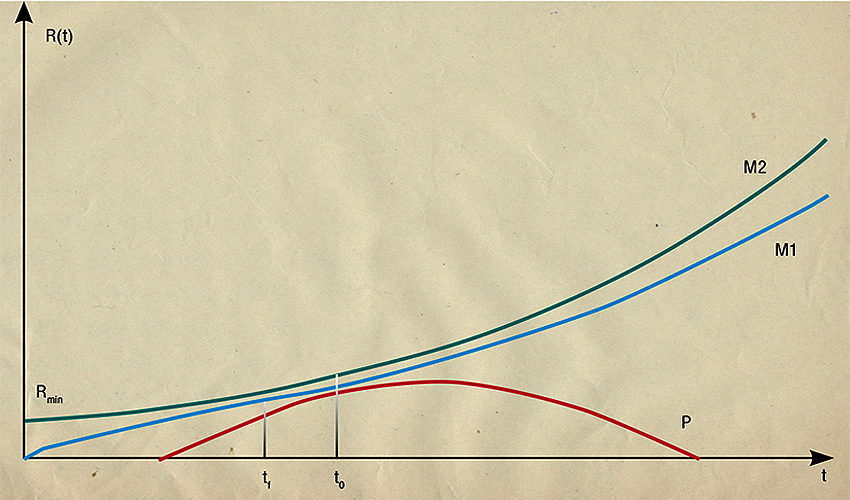
Три возможных главных сценария эволюции космоса, предложенных Фридманом в 1922 г., изображены в виде зависимости космического радиуса от времени. В первом монотонном сценарии, М1, Вселенная расширяется из сингулярности с уменьшающейся скоростью до некоторого момента tf, затем скорость расширения увеличивается. Настоящее время отмечено на графике линией, проходящей через t₀. Сценарий М1 наилучшим образом согласуется с современными астрофизическими наблюдениями. Кривая М2 соответствует сценарию, когда Вселенная начинает расширяться из состояния с ненулевым начальным радиусом Rmin. Периодический сценарий Р соответствует расширению из точки и сжатию обратно в точку. По: (Physics Today, October 2012, p. 38)
Нобелевский предтеча
В книге «Мир как пространство и время», увидевшей свет в 1923 году, сам Фридман рассказывает о Большом взрыве: «Переменный тип Вселенной представляет большое разнообразие случаев; для этого типа возможны случаи, когда радиус кривизны мира, начиная с некоторого значения, постоянно возрастает с течением времени; возможны далее случаи, когда радиус кривизны меняется периодически: Вселенная сжимается в точку (в ничто), затем снова из точки доводит радиус свой до некоторого значения, далее опять, уменьшая радиус своей кривизны, обращается в точку и т. д.».
И, наверное, неожиданно для многих своих читателей Фридман обращается к индусской мифологии о периодах жизни, в которой «появляется возможность также говорить о “сотворении мира из ничего”, но все это пока должно рассматриваться как курьезные факты, не могущие быть солидно подтвержденными недостаточным астрономическим материалом». «Бесполезно, — пишет Фридман, — за отсутствием надежных астрономических данных приводить какие-либо цифры, характеризующие ““жизни” переменной Вселенной; если все же начать подсчитывать ради курьеза время, прошедшее от момента, когда Вселенная создавалась из точки, до теперешнего ее состояния, начать определять, следовательно, время, прошедшее от создания мира, то получатся числа в десятки миллиардов наших обычных лет».
Фридман решил исследовать предположение — что произойдет, если радиус Вселенной будет меняться? Дальше в игру уже вступала математика. Фридман утверждал, что можно найти три класса решений с таким качественным развитием
В 1924 году Фридман предлагает еще одну революционную идею о возможности существования динамической Вселенной с отрицательной кривизной, а значит, бесконечной по объему и неограниченной в пространстве.
Спустя десятилетия космические наблюдения подтвердили, что один из трех сценариев развития космоса, предложенных Фридманом в 1922–1924 годов, оответствует действительности. Трем американским астрономам, обнаружившим ускоренное расширение Вселенной, была присуждена Нобелевская премия по физике за 2011 год. При обосновании важности этого открытия Шведская королевская академия наук сослалась на работы Фридмана.
Гений и революция
Александр Александрович Фридман родился в Санкт-Петербурге в семье артиста кордебалета Императорских Санкт-Петербургских театров и пианистки. Однако маленький Александр с ранних лет увлекался математикой. В школьные и студенческие годы к этому добавилось еще и увлечение астрономией. В 1906 году Александр Фридман окончил с золотой медалью Вторую Санкт-Петербургскую гимназию и поступил на математическое отделение физико-математического факультета Петербургского университета. В том же году 18-летний Александр опубликовал свою первую математическую работу в одном из ведущих научных журналов Германии «Математические анналы» (Mathematische Annalen). Его учителем был блестящий математик Владимир Андреевич Стеклов, имя которого носит сейчас Математический институт Академии наук.
В 1924 году Фридман предлагает еще одну революционную идею о возможности существования динамической Вселенной с отрицательной кривизной, а значит, бесконечной по объему и неограниченной в пространстве
Еще будучи студентом, Фридман написал ряд работ, из которых одна — «Исследование неопределенных уравнений второй степени» — в 1909 году была удостоена золотой медали. В 1910 году Александр окончил Санкт-Петербургский университет и по рекомендации Стеклова был оставлен на кафедре чистой и прикладной математики для подготовки к профессорскому званию. А весной 1913-го, после сдачи магистерских экзаменов, он поступил на работу в Аэрологическую обсерваторию Российской академии наук в Павловске под Петербургом и стал заниматься изучением способов наблюдения атмосферы, динамической метеорологией (теперь эту область науки называют геофизической гидродинамикой). Кроме синоптики и динамической метеорологии ему пришлось ознакомиться с теорией земного магнетизма. Скоро он стал выдающимся специалистом в метеорологии и смежных областях. В 1913 году Фридман напечатал в «Географическом сборнике» очень важную работу «О распределении температуры воздуха с высотою».
Весной 1914 года Фридман был направлен на стажировку в Лейпциг, где в это время жил известный норвежский метеоролог Вильгельм Фриман Корен Бьеркнес, создатель теории фронтов в атмосфере. Летом того же года Фридман летал на дирижаблях, принимая участие в подготовке к наблюдению солнечного затмения в августе 1914 года. С началом Первой мировой войны Фридман вступил добровольцем в авиационный отряд. В 1914–1917 годах он участвовал в организации аэронавигационной и аэрологической службы на Северном, Юго-Западном и других фронтах. Фридман многократно участвовал в качестве летчика-наблюдателя в боевых полетах, в разведывательных операциях.
Освоив профессию летчика, Фридман стал преподавать в школе авиаторов в Киеве. В 1917 году его приглашают для чтения лекций в Киевский университет, а затем он переезжает в Москву, где становится основателем и первым директором завода «Авиаприбор» — первого авиаприборостроительного предприятия в России. Но война подорвала его здоровье, у Фридмана обнаружилась болезнь сердца. Врачи не советовали Фридману жить в Петрограде, куда он хотел было переехать, и он выбрал Пермь. В ноябре 1917-го он подает заявление об участии в конкурсе, а 13 апреля 1918 года занимает должность экстраординарного профессора кафедры механики Пермского университета. До 1920 года профессор Александр Фридман работал проректором Пермского университета, читал курсы дифференциальной геометрии и физики.
В 1920 году Фридман возвращается в Петроград и начинает работать в геофизической обсерватории, а через пять лет становится ее директором. Основной его интерес в то время сосредоточен на аэродинамике и теории турбулентности. О научном энтузиазме и энергии Фридмана говорит такой факт: в июле 1925 года он участвует в рискованном полете на стратостате с целью сбора данных о состоянии атмосферы на больших высотах. Достигнув высоты 7400 метров, он сам и пилот Федосеенко оказываются на волосок от гибели из-за нехватки кислорода.
С началом Первой мировой войны Фридман вступил добровольцем в авиационный отряд. В 1914–1917 годах он участвовал в организации аэронавигационной и аэрологической службы на Северном, Юго-Западном и других фронтах
Основной труд Фридмана по гидромеханике — «Опыт гидромеханики сжимаемой жидкости» (1922). В нем он дал наиболее полную теорию вихревого движения в жидкости, рассмотрел, а для ряда случаев решил важную проблему — возможные движения сжимаемой жидкости при действии на нее определенных сил. Это фундаментальное исследование позволяет считать Фридмана одним из создателей теории сжимаемых жидкостей. В той же работе Фридман вывел общее уравнение для определения скорости вихря, которое приобрело фундаментальное значение в теории прогноза погоды.
Весной 1922 года в главном физическом журнале того времени Zeitschrift fur Physik появилось обращение «К немецким физикам». Правление Германского физического общества извещало о трудном положении коллег в России, которые с начала войны не получали немецких журналов. Поскольку лидирующее положение в тогдашней физике занимали немецкоязычные ученые, речь шла о многолетнем информационном голоде. Немецких физиков просили направлять по указанному адресу публикации последних лет, с тем чтобы потом переслать их в Петроград. Именно в этом журнале, всего двадцатью пятью страницами ниже, была помещена статья, полученная из Петрограда и на первый взгляд противоречащая призыву о помощи. Имя автора — Александр Фридман — физикам было неизвестно. Его статья «О кривизне пространства» касалась общей теории относительности. Точнее, ее самого грандиозного приложения: космологии.
Эйнштейн и судьба
Появившаяся в 1905 году специальная теория относительности была хорошо известна в России. Но статья Эйнштейна, написанная в 1915-м, в которой он сформулировал принципы общей теории относительности, из-за Первой мировой войны дошла до российских ученых с запозданием. Вскоре после окончания войны сообщения об этой теории и о подтверждающих ее наблюдениях солнечного затмения, проведенных Артуром Эддингтоном в мае 1919 года, наконец дошли до России и были с энтузиазмом восприняты научной общественностью.
С 1921 года возобновляется доставка европейских научных публикаций в Россию, и российские ученые получают доступ к необходимой литературе. Кроме того, ценную информацию о новой теории привозит в Петроград физик Всеволод Фредерикс, знавший о ней фактически из первых рук. Во время войны он был интернирован в Германию в качестве «гражданского пленного». По разрешению немецких властей Фредерикс работал в Геттингене ассистентом у Давида Гильберта, в начале 1916 ггода сформулировавшего уравнения общей теории относительности независимо от Эйнштейна, и был очень хорошо знаком с ее принципами.

Всеволод Константинович Фредерикс (1885–1944) — русский физик и геофизик, основатель школы молекулярной физики полимеров и жидких кристаллов Санкт-Петербургского государственного университета
Wikipedia
Фридман очень высоко оценивает работы Эйнштейна. В своей книге «Мир как пространство и время» он напишет: «Теория Эйнштейна оправдывается на опыте; она объясняет старые, казавшиеся необъяснимыми явления и предвидит новые поразительные соотношения. Вернейший и наиболее глубокий способ изучения при помощи теории Эйнштейна геометрии мира и строения нашей Вселенной состоит в применении этой теории ко всему миру и в использовании астрономических исследований. Пока этот метод немногое может дать нам, ибо математический анализ складывает свое оружие перед трудностями вопроса и астрономические исследования не дают еще достаточно надежной базы для экспериментального изучения нашей Вселенной. Но в этих обстоятельствах нельзя не видеть затруднений временных; наши потомки, без сомнения, узнают характер Вселенной, в которой мы обречены жить…»
В тесном сотрудничестве с Фредериксом Фридман и создает свои основополагающие труды по общей теории относительности.
В июне 1922 года Фридман посылает русскоязычный вариант своей работы «О кривизне пространства» в Лейден, нидерландскому физику-теоретику Паулю Эренфесту, который и передает ее для публикации в Zeitschrift für Physik. На статью, вышедшую в свет в июле 1922-го, обращает внимание сам Эйнштейн, что, впрочем, неудивительно — ведь Эренфест был его близким другом.
Оценка Эйнштейном теории Фридмана как «подозрительной» показала, насколько неприемлемой в то время выглядела для него идея об изменяющейся Вселенной. Правильная, по его мнению, теория должна была подтвердить «очевидное» постоянство космоса.

Александр Фридман в двадцатые годы
Wikipedia
В сентябре 1922 года Эйнштейн посылает в Zeitschrift für Physik короткую заметку, в которой высказывает предположение, что Фридман допустил математическую ошибку. В ответном письме, датированном декабрем 1922-го, Фридман приводит свои выкладки более подробно. Однако это письмо попадает в руки адресата только в мае следующего года, когда Эйнштейн возвращается из своего лекционного турне вокруг света.
Месяцем позже коллега Фридмана советский физик Юрий Александрович Крутков встречается с Эйнштейном в доме Эренфеста в Лейдене и дает последние разъяснения. Сразу же после этой встречи Эйнштейн публикует в Zeitschrift für Physik еще одно сообщение, в котором признает математические выкладки Фридмана верными. Правда, в черновике он все-таки отмечает, что «решение не имеет физического смысла», но, поразмыслив, вычеркивает неосторожную ремарку.
Тем не менее должно было пройти еще восемь лет, прежде чем Эйнштейн согласился с идеей расширяющейся Вселенной.
Эйнштейн публикует в Zeitschrift für Physik еще одно сообщение, в котором признает математические выкладки Фридмана верными. Правда, в черновике он все-таки отмечает, что «решение не имеет физического смысла», но, поразмыслив, вычеркивает неосторожную ремарку
Параллельно Фридман выдвигает еще один аргумент против идеи о замкнутом космосе. По предложению своего давнего друга математика Якова Тамаркина он задается вопросом: имеются ли у уравнений общей теории относительности решения в виде бесконечного по объему гиперболоида с одинаковой отрицательной кривизной в каждой точке пространства?
В своей новой статье, опубликованной в Zeitschrift für Physik в январе 1924-го, он приводит два таких решения: статическое и динамическое. Статическое решение для пространства с отрицательной кривизной, как и решение де Ситтера, требует нулевой плотности вещества во Вселенной, а значит, не представляет физического интереса. В случае динамического решения плотность материи должна быть такой же, как и в варианте с положительной кривизной. Из чего, например, следует, что невозможно определить знак кривизны пространства на основе одного лишь измерения плотности вещества.
К сожалению, эта статья Фридмана также была проигнорирована международным физическим сообществом, включая Эйнштейна.
К несчастью, жизнь Александра Фридмана оборвалась в самом ее разгаре — в сентябре 1925 года он, вернувшись из Крыма, заболевает брюшным тифом и после двух недель борьбы с недугом умирает в возрасте 37 лет.
Жизнь после смерти
В 1927 году бельгийский физик и священник Жорж Леметр переоткрывает уравнения Фридмана и решает их. Он приходит к пониманию, что Вселенная, скорее всего, расширяется. Поэтому он называет свою работу «Об однородной Вселенной с постоянной массой и увеличивающимся радиусом». Но вместо того, чтобы рассмотреть всевозможные сценарии, он выбирает предельный случай монотонного мира — М2 по классификации Фридмана, в котором размер Вселенной логарифмически медленно возрастает от радиуса Эйнштейна до бесконечности. Этот сценарий, как потом выяснилось, не является физически состоятельным.
В 1927 году бельгийский физик и священник Жорж Леметр переоткрывает уравнения Фридмана и решает их. Он приходит к пониманию, что Вселенная, скорее всего, расширяется
В 1929 г. Эдвин Хаббл построил график зависимости скорости удаления галактик от расстояния до них и обнаружил, что зависимость носит линейный характер.
Леметра, опубликовавшего свои открытия в малоизвестном журнале Бельгийской академии наук, ждала судьба Фридмана: никто из корифеев, даже его бывший учитель Артур Эддингтон, не проявляет интереса к его идеям. На конференции в Сольвее в 1927 году Эйнштейн сообщил Леметру, что Фридман уже получил эти решения раньше, и назвал идею расширяющейся Вселенной abominable (буквально: «отвратительной»).
В 1929 году Хаббл оценивает с помощью специальной техники расстояния до 46 галактик и, располагая на графике их скорости, полученные Слайфером, в зависимости от своих расстояний до них, обнаруживает, что полученные точки лежат достаточно близко от прямой. Наклон этой прямой и получает название постоянной Хаббла.
В начале 1931 года Эйнштейн отправляется в калифорнийскую обсерваторию Маунт-Вильсон, чтобы лично поговорить с Хабблом и обсудить его результаты. Вернувшись в Берлин, он пишет работу, где признает теорию расширения Вселенной, отмечая приоритет Фридмана
Дольше всех противится новой теории Эйнштейн, но и его мнение постепенно меняется, чему способствуют публикация результатов Хаббла и найденное Эддингтоном в том же году доказательство нестабильности статического решения самого Эйнштейна, даже при наличии положительной космологической постоянной.
В начале 1931 года Эйнштейн отправляется в калифорнийскую обсерваторию Маунт-Вильсон, чтобы лично поговорить с Хабблом и обсудить его результаты. Вернувшись в Берлин, он пишет работу, где признает теорию расширения Вселенной, отмечая приоритет Фридмана.















![R_{{ij}}={frac {partial Gamma _{{ki}}^{{k}}}{partial x^{j}}}-left[{frac {partial Gamma _{{ij}}^{{k}}}{partial x^{k}}}+{frac {partial Gamma _{{ij}}^{{0}}}{partial t}}right]+Gamma _{{ik}}^{0}Gamma _{{j0}}^{k}+Gamma _{{i0}}^{k}Gamma _{{jk}}^{0}+Gamma _{{ik}}^{l}Gamma _{{jl}}^{k}-(Gamma _{{ij}}^{k}Gamma _{{kl}}^{l}+Gamma _{{ij}}^{0}Gamma _{{0l}}^{l})](https://wikimedia.org/api/rest_v1/media/math/render/svg/3168e3c16a7d82bbbe468315326e8836c4efce8f)

















































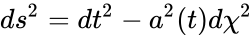
 , где компоненты метрического тензора равны:
, где компоненты метрического тензора равны: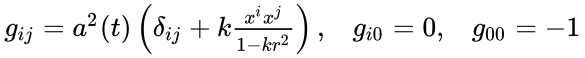 ,
,

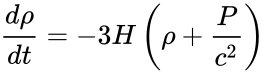
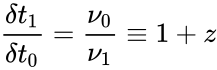
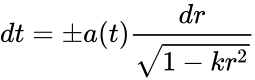
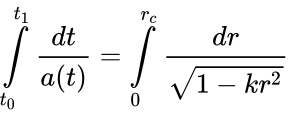

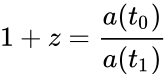
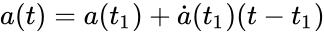
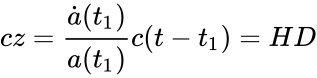
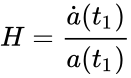
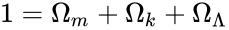 ,
,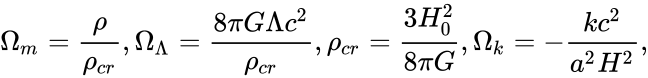
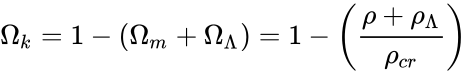 ,
,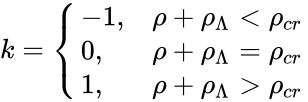
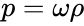 (1)
(1)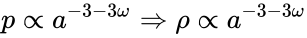
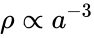
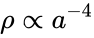

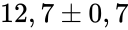 млрд лет[15], однако, результат оспаривается. Оппоненты указывают, что не были учтены дополнительные источники ошибок, их оценка
млрд лет[15], однако, результат оспаривается. Оппоненты указывают, что не были учтены дополнительные источники ошибок, их оценка 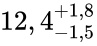 млрд лет[16].
млрд лет[16].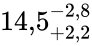 [18] млрд лет — вторым.
[18] млрд лет — вторым.