Сценарий рюэля такенса

Лекция 14

Сценарии
перехода к хаосу. Общая дискуссия

Как известно, в уравнениях динамических
систем обычно присутствуют параметры
– величины, которые считаются постоянными
во времени, но от задания которых может
зависеть характер реализующегося в
системе режима. Можно представить себе,
что система заключена в черный ящик, на
котором имеется несколько ручек
настройки. Предположим, что при одном
положении ручек наблюдается регулярный
режим дина­мики, например, периодические
колебания, а при другом – хаос. Если мы
плавно меня­ем настройку так, чтобы
перейти от первой ситуации ко второй
(рис.14.1), то какой будет на пути к хаосу
последовательность бифуркаций –
событий, состоящих в качест­венном
изменении характера наблюдаемого
режима? Об этой последовательности
бифуркаций принято говорить как о
сценарии перехода к хаосу. При этом
подразуме­вается, что имеется
сравнительно немного сценариев,
являющихся в определенном смысле слова
типичными, так что проблема их классификации
и изучения не является необозримой.

Рис.14.1. К понятию
сценария перехода к хаосу.

Общепризнанно, что отправным пунктом
в исследовании проблемы перехода к
хаосу служит работа Л.Д.Ландау,
опубликованная в 1944 г. В ней ставится
вопрос о том, как возникает турбулентность
при увеличении числа Рейнольдса,
основного упра­вляющего параметра в
гидродинамических задачах. Согласно
предложенному Ландау сценарию, первичное
течение теряет устойчивость по отношению
к колебательному возмущению на некоторой
частоте, затем возникшее осциллирующее
течение в свою очередь становится
неустойчивым по отношению к возмущению
на другой частоте и так далее. В результате
большого числа бифуркаций, которые
сопровождаются возник­новением все
новых и новых частот, находящихся в
иррациональных отношени­ях, возникает
сложный динамический режим –
турбулентность. Несмотря на то, что речь
идет о гидродинамической турбулентности,
аргументация носит столь общий характер,
что ее можно с равным основанием отнести
и к другим диссипативным динамическим
системам с многомерным фазовым
пространством. Несколько позднее
аналогичные представления были развиты
немецким математиком Эберхардом Хопфом
(Hopf, 1948). Он предложил также конкретную
модельную систему, демонстриру­ющую
усложнение динамики в результате
последовательного рождения составляющих
с несоизмеримыми частотами.

В начале 70-х годов анализ Ландау и Хопфа
был подвергнут критике в работе
иссле­дователей из Франции и Голландии
Дэвида Рюэля и Флориса Такенса.
Согласно их утверждению, после рождения
первых трех (в другой версии теоремы –
после четырех) составляющих с несоизмеримыми
частотами может возникать странный
аттрактор, который характеризуется
неустойчивостью принадлежащих ему
фазовых траекторий (Ruelle,
Takens, 1971, Newhouse, Ruelle, Takens, 1978). По Рюэлю
и Такенсу, странный аттрактор и есть
математический образ турбулентного
движения. Ситуация, когда имеет место
большее число бифуркаций не то чтобы
невозможна, но атипична, т.е. практически
невероятна.

Хотя в литературе часто встречается
словосочетание «сценарий Рюэля и
Такенса», его нельзя признать вполне
правомерным, поскольку на самом деле
они не дали явного описания последовательности
бифуркаций на пути от порядка к хаосу.
Что же в действительности ими было
доказано? Если сформулировать основной
результат на физическом языке, то он
сводится к следующему. Пусть мы имеем
M3 диссипативных
систем, каждая из которых демонстрирует
периодические автоколебания на своей
частоте, причем все частоты находятся
в иррациональных отношениях. В этом
случае система, составленная из
несвязанных подсистем, будет иметь
аттрактором M-мерный тор. Введем
теперь связь между подсистемами. Согласно
Рюэлю и Такенсу, при сколь угодно малой
величине связи можно так подобрать вид
этой связи, что реализуется странный
аттрактор, и динамика будет хаотической.
Ими доказан даже более сильный результат.
Представим себе пространство функций,
которые стоят в правых частях динамических
уравнений системы. Утверждается, что в
этом пространстве множество точек,
соответствующих хаотической динамике,
является всюду плотным в сколь угодно
малой окрестности точки, отвечающей
отсутствию связи.

Первоначальная интерпретация работы
Рюэля и Такенса некритически настро­енными
исследователями состояла в том, что
появление третьей частотной состав­ляющей
в наблюдаемом спектре колебаний системы
должно сопровождаться не­медленным
рождением хаоса. Как выяснилось, проблема
на самом деле оказалась куда более
сложной и тонкой.

Во-первых, были приведены убедительные
примеры реалистичных систем, в ко­торых,
в противоположность заключениям Рюэля
и Такенса, наблюдаются квазипери­одические
режимы с числом несоизмеримых частот
более 3 (Tavakol, Tworkowski, 1984, Grebogi
et al., 1985, C. Baesens et al., 1991). Оказалось,
что при достаточно слабой связи подсистем
это весьма распространенная ситуация.

В работе Grebogi
et al., 1985 был
предпринят численный эксперимент с
модельной системой, описывающей динамику
с тремя несоизмеримыми частотами:

(14.1)

где переменные 
и 
имеют смысл фаз, одна частота отвечает
шагу дискретного времени, а вторая и
третья задаются, соответственно,
параметрами
w₁
и w₂.
Функции

и

имеют период 2
по каждому аргументу и представляются
рядами Фурье. Была проведена большая
серия расчетов. Задав величины
коэффициентов Фурье и параметры w₁
и w₂
случайным образом, исследователи
определяли характер реализующегося
режима по показателям Ляпунова:

• _1,2<0–
  периодический,

• ₁=0,
  ₂<0
  – 2–х частотный квазипериодический,
  2-тор,

• ₁=0,
  ₂=0
  – 3–х частотный квазипериодический,
  3-тор,

• ₁>0
  – хаос.

На рис.14.2 приведена
диаграмма, на которой сопоставляется
относительная доля испытаний, в кото­рых
обнаруживался тот или иной тип режима.
При малом уровне возмущения k
доминирует
трехчас­тотная квазипериодичность.
С ростом уровня возмущения растет доля
периодических и хаотических режимов.
При k>k_c,
где k_c
отвечает
моменту потери обратимости модельного
отображения, трехчастотная квазипериодичность
становится невозможной.

Надо подчеркнуть,
что сказанное противоречит не утверждению
теоремы Рюэля и Такенса, как тако­вой,
а, скорее, интерпретации понятия
типичности, которое оказалось не вполне
адекватным. Действи­тельно, всюду
плотное множество совсем не обязательно
имеет заметно отличную от нуля меру.
Поэтому присутствие в пространстве
систем плотного множества, отвечающего
наличию хаоса, еще не означает, что хаос
будет наблюдаться с высокой вероятностью.

Рис.14.2. Относительная
доля испытаний, в которых обнаруживался
различный тип режима при случайном
выборе параметров и функций в модельном
отображении (14.1) (Grebogi
et al., 1985).
Величина параметра k=k_c
отвечает
моменту потери обратимости отображения.

Во-вторых, после опубликованной в 1984 г.
работы группы из Мэрилендского
университета (Grebogi et al, 1984) и последующих
исследований стало ясно, что сцена­рий
перехода к хаосу через квазипериодические
режимы может включать, как проме­жуточный
этап, образование странных нехаотических
аттракторов. В ин­терпре­тации
мэрилендской группы, термин «странный»
относится к геометри­ческой структуре
аттрактора, который представляет собой
фрактальный объект, а термин «нехаотический»
указывает на отсутствие чувствительной
зависимости динамики от начальных
условий: среди ляпуновских показателей
аттрактора нет положительных.

С другой стороны, подвергнутое критике
предположение о том, что число бифурка­ций
на пути к хаосу может быть бесконечным,
оказалось справедливым, хотя и для
другого сценария. Речь идет переходе к
хаосу через каскад (бесконечную
последова­тельность) бифуркаций
удвоения периода. Около 1976 г. американский
физик Митчел Фейгенбаум, работавший в
Лос-Аламосской национальной лабора­тории
США, обнару­жил ряд замечательных
закономерностей, сопровождающих этот
тип перехода к хаосу (Feigenbaum 1978, 1979). О нем
говорят теперь как о сценарии
Фейгенбаума, и это наименование можно
считать заслуженным. Хотя Фейгенбаум
не является первооткры­вателем
удвоений периода, описанных и изу­чавшихся
до него многими исследова­телями
(May, 1986), он первым осознал прису­щие
этому сценарию свойства универ­сальности
и скейлинга (масштабного подобия)
и разработал их теоретическое обосно­вание,
привнеся в нелинейную динамику метод
ренормализационной группы (сокра­щенно
ренормгруппы или РГ).

Сущность концепции универсальности
состоит в том, что имеется обширное
мно­жество нелинейных диссипативных
систем различной природы (класс
универ­саль­ности), которые не
просто демонстрируют одну и ту же
последовательность бифурка­ций, но
проявляют у порога возникновения хаоса
одни и те же количест­венные
закономерности скейлинга, с присущими
данному классу универсальности
определен­ными значениями масштабных
констант.

Метод ренормгруппы, концепции
универсальности и скейлинга ранее были
развиты в теории фазовых переходов. В
1982 г. вклад американский физик Кеннет
Вильсон получил Нобелевскую премию за
вклад в разработку этих концепций. При
приближе­нии температуры вещества к
критической точке фазового перехода
T_с корреляционная длина
флуктуаций возрастает и становится
большой по сравне­нию с межатомным
расстоянием. В широком интервале
пространственных мас­штабов поведение
флуктуа­ций становится не зависящим
от их масштаба и не чувствительным к
деталям межатом­ных взаимодействий,
приобретая универ­сальные свойства.
Помимо прочего, это делает продуктивным
изучение фазовых переходов с помощью
модельных систем, огрубляющих детали
локальных взаимо­действий из соображений
удобства анализа, но сохраняющих
интересующий тип критического поведения.

Как оказалось, аналогичный подход
плодотворен и в нелинейной динамике
при рассмотрении проблемы возникновения
хаоса. Представим себе динамическую
систе­му, в которой при переходе
параметра через некоторое критическое
значение наблюда­ется мягкое (без
скачка) рождение хаоса. В силу непрерывности
динами­ческих уравнений по параметру,
обнаружить различие между регулярным
и хаоти­ческим режимами, реализующимися
в -окрестности точки
перехода, можно толь­ко при их наблюдении
за достаточно большое время T().
Очевидно, при

имеем
.
Сужая рассматриваемую окрестность
критической точки, можно добиться того,
чтобы временной масштаб T()
намного превышал все величины с
размерностью времени, фигурирующие в
уравнениях системы. С точки зрения
трансформации природы режима в узкой
окрестности точки перехода, локальные
во времени детали динамики, как можно
ожидать, становятся не существенными,
и собственно переход должен носить
универсальный характер.¹
В этом случае для феноменологического
описания динамики нелинейных систем у
порога хаоса естественно использовать
наиболее простые модели, обладающие
нужным типом критического поведения,
т.е. правильно передающие динамику на
больших вре­менных масштабах. Ясно,
что конструирование таких моделей
следует рассма­тривать как одну из
важных задач теории.

В контексте нелинейной динамики и
перехода к хаосу идея метода ренорм­группы
состоит в следующем. Предположим, что
мы имеем зависящий от пара­метров
оператор, описывающий эволюцию состояния
динамической системы на некотором
временном интервале. Используя его, мы
можем построить оператор эволюции на
некотором большем временном интервале.
Далее посредством мас­штабных замен
переменных мы стараемся добиться того,
чтобы новый оператор эволюции по
возможности совпадал со старым. Если
при некоторых значениях параметров это
удается сделать, то процедуру можно
повторять многократно, получая
последователь­ность операторов
эволюции для все больших и больших
временных интервалов. Процедура перехода
от старого оператора к новому,
перенормированному, называется РГ
преобразованием, а набор значений
парамет­ров, о котором мы говорили,
задает расположение критической точки.
В крити­ческой точке структура
операторов эволю­ции на больших
временах оказывается обусловленной не
конкретным видом исходного оператора
системы, а структурой РГ преобразования.
В этом и состоит универсаль­ность.
Поскольку в критической точке получаемые
при многократном применении РГ
преобразования операторы эволюции
оказываются одинаковыми с точностью
до масштабной замены пере­менных,
система должна демонстрировать на
различных временах подобную динамику
с соответствующим пересчетом масштаба
динамических переменных, проявляя
свойство скейлинга. При выходе по
параметрам из критической точки
возникающее возмущение оператора
эволюции будет трансформироваться при
итерациях РГ преобразования вполне
определенным, универсальным обра­зом.
В результате топография пространства
параметров вблизи критической точки
также обладает свойствами универсальности
и скейлинга.

Работа Фейгенбаума показала, что проблема
сценариев возникновения хаоса не
ограничивается качественной стороной,
т.е. не сводится к перечислению возмож­ных
последовательностей бифуркаций, а имеет
количественный аспект. Закономер­ности,
аналогичные фейгенбаумовским, но
характеризуемые другими значениями
масштаб­ных констант, были в дальнейшем
обнаружены для целого ряда типов
критического поведения, возникающих
при многопараметрическом анализе
возникновения хаоса через удвоения
периода (Kuznetsov et al., 1997, Кузнецов
и др., 1997). Количественные закономерности
и универсальные константы найдены также
для многих ситуаций, отвечающих пере­ходу
к хаосу через квазипериодические режимы
(Shenker, 1982, Feigenbaum et al., 1982, Rand et
al, 1982), хотя в этом случае полная
картина оказывается очень сложной, и
многие ее аспекты остаются до сих пор
до конца не изученными.

Рис.14.3. Перемежающаяся
турбулентность в гидродинамическом
течении.

В 1980 г. появилось сообщение французских
исследователей И.Помо и П.Манневилля,
положившее начало изучению группы
сценариев перехода к хаосу через
перемежаемость (Pomeau, Manneville,
1980). В гидродинамике давно известна
так называемая перемежающаяся
турбулентность, когда течение в
определенных пространственных областях
имеет плавный, ламинарный характер, но
они чередуются с областями нерегулярного,
турбулентного течения. Благодаря тому,
что турбулентные области перемещаются,
меняют форму, возникают и исчезают,
перемежающийся характер носит также
зависимость наблюдаемых величин от
времени в фиксированной точке пространства
(рис.14.3). Помо и Манневилль указали
нес­колько возможных ситуаций, когда
в динамических системах (в том числе со
срав­нительно небольшой размерностью
фазового пространства) может возникнуть
пе­ремежаемость, и наметили классификацию,
введя в рассмотрение три типа
переме­жаемости. В дальнейшем свойства
такого рода переходов были исследованы
более подробно. В частности, для
перемежаемости типа I и III был развит
ренорм­групповой анализ, аналогичный
теории Фейгенбаума.²

Итак, в итоге изучения вопроса о переходе
динамических систем к хаосу, сложи­лось
представление о трех основных сценариях,
а именно, через каскад удвоений периода,
перемежаемость и квазипериодические
режимы. Оставшаяся часть наше­го курса
будет посвящена рассмотрению этих
сценариев и, соответствующих им
особенностей сложной динамики нелинейных
систем в области перехода от порядка к
хаосу.

Обсудим, почему типичными оказываются
именно перечисленные выше сценарии и
в каком отношении друг к другу они
находятся.

Предположим сначала, что в системе
реализуется простейший устойчивый
пе­риодический режим динамики, т.е.
предельный цикл. Чтобы увидеть, что с
ним мо­жет произойти при изменении
параметров, воспользуемся методом
сечения Пуан­каре. Пусть для простоты
цикл «живет» в трехмерном фазовом
пространстве (рис.14.4), тогда имеем
двумерное отображение Пуанкаре

. (14.2)

Точка, где предельный цикл протыкает
поверхность сечения, есть неподвижная
точка этого отображения:
.
Исследование на устойчи­вость
заключается в том, что мы подставляем
в (14.2)

и, удерживая члены первого порядка,
получаем

, (14.3)

где

– матрица Якоби. Рассмотрим задачу на
собственные векторы и собственные
значения этой матрицы:

,
s=1,2. (14.4)

Если ввести след и детерминант матрицы
,
соответственно,

и
, (14.5)

то собственные числа получаются как
корни квадратного уравнения

. (14.6)

Именно,

. (14.7)

Произвольный вектор возмущения
представляется в виде линейной комбинации
двух собственных векторов. При каждом
обходе предельного цикла возмущение,
отвечающее каждому собственному вектору,
умножается на соответствующее собственное
число – мультипликатор .
Поэтому цикл устойчив, если оба
мульти­пликатора по модулю меньше
единицы, и неустойчив, если хотя бы один
мульти­пликатор по модулю больше
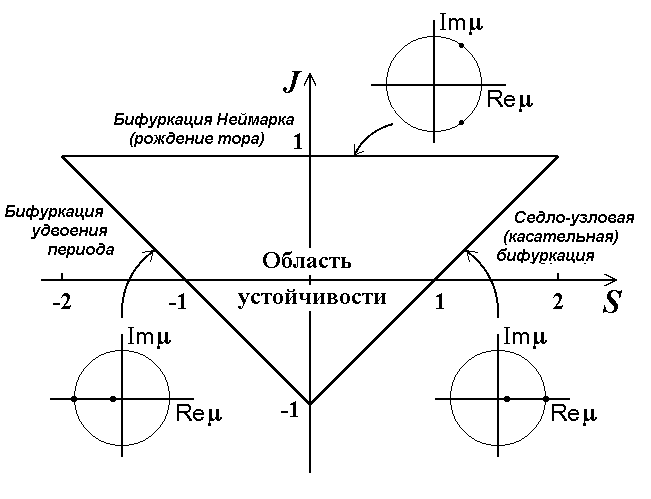
единицы. Две пограничные линии области
устойчи­вости на плоскости (S,J)
можно получить из (14.6), полагая =1
или =–1, что дает,
соответственно,

(14.8)

и

. (14.9)

Третья пограничная линия находится из
соотношения (14.7): если под знаком
квадратного корня стоит отрицательное
число, то модуль мультипликатора будет
единичным при

. (14.10)

Область внутри треугольника, образованного
линиями (14.8)–(14.10), есть область
устойчивости.

Предположим, что наша система содержит
параметр A.
Когда мы варьируем этот параметр,
будут изменяться координаты неподвижной
точки x₀,
y₀,
и, соответственно, след и детерминант
матрицы Якоби: S=S(A),
J=J(A).
При этом на плоскости (S,J)
мы будем двигаться вдоль некоторой
кривой. Ясно, что типичным надо признать
выход из треугольника устойчивости
через одну из его сторон (рис.14.4).

Рис.14.4. Область
устойчивости предельного цикла на
плоскости след – детерминант матрицы
Якоби.

Предположим сначала, что выход
осуществляется через левую границу
треу­гольника. На пороге потери
устойчивости мультипликатор равен
минус единице. Это значит, что при
однократном обходе цикла малое возмущение
меняет знак (рис.14.5 а). Чтобы траектория
замкнулась, нужно совершить еще один
обход, так что период вновь возникшего
движения оказывается вдвое больше, чем
у исход­ного.

Если присущая системе нелинейность
такова, что при увеличении амплитуды
возмущения происходит его стабилизация,
то результатом бифуркации будет рождение
цикла с периодом вдвое больше исходного.
Это бифуркация удвоения периода. Очень
часто при дальнейшем изменении параметра
за ней вновь следуют бифуркации такой
же природы. Последовательность
бифуркационных значений параметра
накапливается к определенному пределу,
критической точке, которая является в
определенном смысле границей хаоса.
Это сценарий перехода к хаосу через
каскад бифуркаций удвоения периода
–сценарий Фейгенбаума.

а)
б) в)

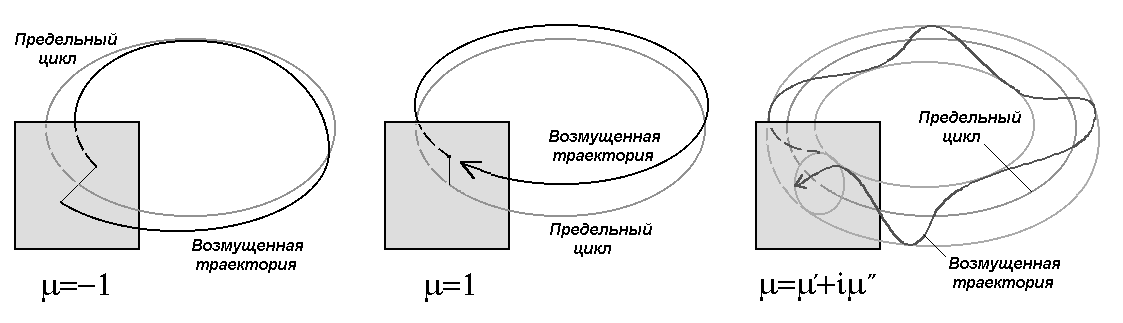
Рис.14.5. Поведение
близкой к предельному циклу траектории
на трех границах треугольника устойчивости.

Может встретиться другая ситуация,
когда нелинейность способствует
ускоре­нию роста возмущения и уходу
системы от ставшей неустойчивой
периодической орбиты. В этом случае,
когда мы подходим к точке бифуркации,
к рассматри­ваемому циклу приближается
неустойчивый цикл удвоенного периода,
который сливается с исходным циклом в
точке бифуркации и, как говорят, передает
ему свою неустойчивость. После бифуркации
наблюдается уход близлежащих траек­торий
от неустойчивого цикла в удаленные
области фазового пространства. Мо­жет
случиться, что динамика в этих удаленных
областях такова, что через некото­рое
время траектория возвращается в
окрестность потерявшей неустойчивого
цикла, тогда она останется вблизи него
в течение некоторого времени, вновь
уйдет, затем вновь вернется и т.д. Если
такая реинжекция траектории в окрестность
неустойчивого цикла имеет место, и если
динамика в удаленных областях фазового
пространства характеризуется наличием
неустойчивости по отношению к возмущению
начальных условий, то это приводит к
возникновению хаотического режима
перемежающегося типа. Помо и Манневилль
обозначают его как перемежаемость типа
III.

Рассмотренные варианты бифуркаций
наглядно иллюстрируются с помощью
одно­мерных отображений (рис.14.6 и
14.7). Такая возможность связана с тем,
что анализируемая граница потери
устойчивости пересекает ось J=0,
которую можно трактовать как соответствующую
случаю одномерных отображений.

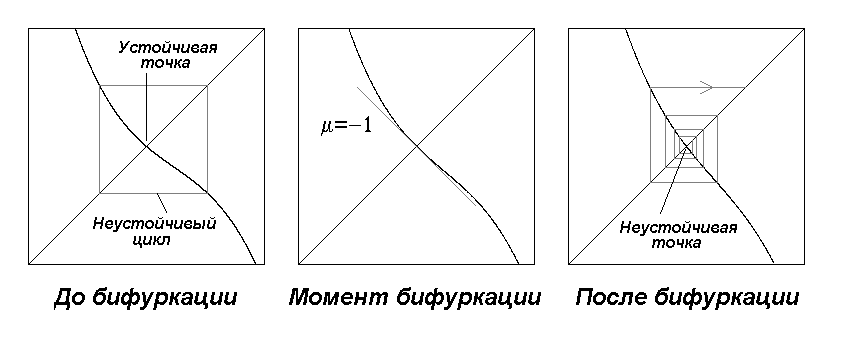
Рис.14.6. Бифуркация
удвоения периода (мягкая, нормальная,
суперкритическая).

Рис.14.7. Субкритическая
бифуркация удвоения периода.

Пусть теперь выход из треугольника
устойчивости осуществляется через
правую сторону. Тогда на пороге потери
устойчивости мультипликатор обращается
в плюс единицу. При однократном обходе
цикла возмущенная траектория почти
замыкается (рис.14.5 б). Чтобы выяснить,
как трансформируется динамика, оказывается
необхо­димым обязательно учитывать
нелинейность. Когда мы движемся к точке
бифуркации, к устойчивому предельному
циклу приближается неустойчивый цикл;
в точке бифуркации оба цикла сливаются
и исчезают. Таким образом, в рассматриваемой
области фазового пространства вообще
не остается периодических орбит.

Проясняет ситуацию рассмотрение
одномерного отображения. (Это оправдано,
поскольку, как и в предыдущем случае,
рассматриваемая сторона треугольника
устойчивости пересекает ось J=0.)
График отображения до бифуркации,
в момент ее и после нее показан на
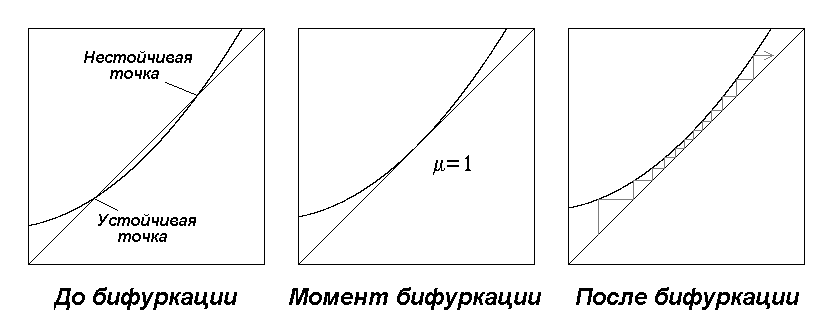
рис.14.8. Для одномерного отображения
бифуркация состоит в слиянии и исчезновении
пары неподвижных точек. В момент
бифуркации график касается биссектрисы,
что определяет ее название – касательная
бифуркация. После бифуркации на месте
исчезнувшей пары неподвижных точек
остается узкий «коридор», прохождение
которого изображающей точкой требует
тем большего числа итераций, чем ближе
мы находимся к точке бифуркации. После
прохождения «коридора» траектория
уходит в удаленные области фазового
пространства. Если динамика в этих
удаленных областях характеризуется
неустойчивостью по отношению к возмущению
начальных условий и если обеспечена
реинжекция, т.е. через некоторое время
траектория оказывается вновь на входе
в «коридор», то наблюдается переход к
хаосу через перемежаемость типа I
по Помо и Манневиллю. Прохождение
через «коридор» интерпретируется как
ламинарная стадия процесса, а блуждание
в удаленных областях фазового пространства
как турбулентная стадия.

Рис.14.8. Касательная
бифуркация.

Наконец, третий вариант выхода из
треугольника устойчивости отвечает
пересе­чению его верхней границы. При
этом пара комплексно-сопряженных
мультипли­каторов 
и * переходит через
единичную окружность. Возмущенная
траектория извивается вокруг теряющего
устойчивость предельного цикла (рис.14.5
в), причем угол поворота за один обход
определяется аргументом комплексного
числа . Как видно
из соотношения (14.7),,
так что аргумент зависит от того, в какой
именно точке мы пересекаем сторону
треугольника. Если величина

выражается рациональным числом p/q,
то возмущенная орбита замыкается после
q обходов.

Как и в случае =–1,
результат бифуркации определяется тем,
способствует нелинейность стабилизации
возмущения или же его усилению.

В первом случае происходит мягкая
бифуркация рождения тора, если

иррациональное число, или периодической
орбиты – резонансного цикла на торе,
если оно рациональное. Области
периодичности имеют вид языков, подходящих
сверху к линии J=1,
а в промежутках между языками реализуются
квазиперио­дические режимы. Бифуркация
рождения тора из предельного цикла
носит название бифуркации Неймарка.
Дальнейшая эволюция аттрактора при
изменении управляющего параметра может
быть разнообразной и сложной, но в общем
можно сказать, что реализуется та
ситуация, о которой говорят как о переходе
к хаосу через квазипериодичность.

Рис.14.9. Различные
пути потери устойчивости предельного
цикла и ассоциирующиеся с ними сценарии
возникновения хаоса.

Второй случай, когда нелинейность
способствует раскачке возмущений,
отвеча­ет уходу траектории от
потерявшего устойчивость предельного
цикла в отдален­ные области фазового
пространства. Если динамика там
хаотическая и если имеет место реинжекция
с возвратом траектории в окрестность
неустойчивого цикла, то реализуется
перемежаемость типа II по
Помо и Манневиллю. Это наиболее сложный
и наименее изученный из трех типов
перемежаемости.

Сводка всех перечисленных возможностей
потери устойчивости предельного цикла
и ассоциирующихся с ними сценариев
возникновения хаоса дается рисунком
14.8.

Оказывается, что и при большей размерности
фазового пространства проведен­ный
анализ остается в силе, в том смысле,
что типичными остаются три варианта
линейной потери устойчивости предельного
цикла (с переходом мультипликатора
через единицу, минус единицу, или пары
комплексно-сопряженных мультипликаторов
через единич­ную окружность) и те же
варианты действия нелинейности на
динамику возмущений вблизи бифуркаций,
какие мы обсудили. Поэтому намеченная
классификация сценари­ев перехода к
хаосу оказывается весьма общей. В
следующих лекциях мы обратимся к более
детальному рассмотрению различных
аспектов динамики, связанной с этими
сценариями.

Такенс

Cтраница 2

В этом случае утвердительный ответ доказан Такенсом ( F. Takens, 1973) [ 14: 90 ] для ростков класса W на прямой и ростков класса W % на плоскости.
 [16]

Коразмерность множества топологически нестабилизируе-ных струй в теореме Такенса ( рассматриваемого как подмножество пространства струй с особой точкой 0) равна трем. Топологическая классификация ростков векторных полей, принадлежащих некоторому подмножеству коразмерности 6, может даже иметь числовые модули.
 [17]

Из трех обычных механизмов только механизм Рюэлля — Такенса не чувствителен к действию ( малого) шума. Кифер доказал, грубо говоря, что для систем с аттрактором, удовлетворяющим аксиоме А, стационарная плотность вероятности системы, возмущаемой цветным внешним шумом, слабо сходится к инвариантной мере аттрактора, когда интенсивность шума стремится к нулю.
 [18]

Рассмотрим примеры, связанные с применением процедуры Паккарда — Такенса для: 1) идентификации размерности математической модели и 2) диагностики объекта управления.
 [20]

Следовательно, трехслойные сети фактически воплощают основное требование теоремы Такенса: проецирование аппроксимация. Комбинация двух проекторов эквивалентна некоторому третьему проектору, а комбинация двух линейных аппроксимаций снова дает линейную аппроксимацию.
 [21]

Хотя в литературе часто встречается словосочетание сценарий Рюэля и Такенса, его нельзя признать вполне правомерным, поскольку на самом деле они не дали явного описания последовательности бифуркаций на пути от порядка к хаосу. Что же в действительности ими было доказано. Если сформулировать основной результат на физическом языке, то он сводится к следующему. Пусть мы имеем М 3 диссипативных систем, каждая из которых демонстрирует периодические автоколебания на своей частоте, причем все частоты находятся в иррациональных отношениях. В этом случае система, составленная из несвязанных подсистем, будет иметь аттрактором М — мерный тор.
 [22]

Надо подчеркнуть, что сказанное противоречит не утверждению теоремы Рюэля и Такенса, как таковой, а, скорее, интерпретации понятия типичности, которое оказалось не вполне адекватным. Действительно, всюду плотное множество совсем не обязательно имеет заметно отличную от нуля меру. Поэтому присутствие в пространстве систем плотного множества, отвечающего наличию хаоса, еще не означает, что хаос будет наблюдаться с высокой вероятностью.
 [23]

Зависимости v от размерности фазового пространства сконструированных на основе процедуры Паккарда — Такенса динамических систем для рассмотренных двух случаев ( 2, 3) и для белого шума ( 1) продемонстрированы на рис. 9.127. Как видно из рисунка, для белого шума тоже наблюдается небольшое насыщение размерности с ростом п, которое связано с ограниченностью числа выборок, но не столь явное, как для экспериментальных реализаций исследуемых процессов.
 [24]

Интерес к маломодовому хаосу инициирован известными работами Лоренца [104], а также Рюзля и Такенса [117], в которых был поставлен общий вопрос: можно ли связать стохастические режимы в распределенной системе, имеющей бесконечно много степеней свободы, с наличием странного аттрактора в системе небольшого числа обыкновенных дифференциальных уравнений, представляющей упрощенную модель исходной системы. В ряде случаев это действительно удается сделать. Точнее говоря, в [5] численными методами был обнаружен странный аттрактор в трехмерной системе, получающейся из уравнения (13.127), дополненного граничными условиями Неймана на отрезке, в результате двухмодовой галеркинской аппроксимации. Другой пример — работа [19], в которой представлен численный анализ странных аттракторов простейших конечно-разностных аппроксимаций краевых задач вида (19.5) на отрезке.
 [25]

Некоторые экспериментальные данные свидетельствуют о том, что сценарий перехода к хаосу Рюэля — Такенса, по-видимому, действительно выполняется для ряда систем.
 [26]

Длина выборки и точность измерений предполагается достаточной для применимости методов нелинейной динамики, в частности, реконструкции по Такенсу. Это предположение может быть подвергнуто проверке, для чего предлагался ряд оценок [323, 192, 266] и методик выбора параметров реконструкции.
 [27]

В фазовом пространстве появлялся трехмерный тор, жесткое разрушение которого приводило к рождению странного аттрактора — реализовывался механизм Рюэля Такенса.
 [28]

На рис. 6.136 видно, что размерность достигает асимптотического значения d 2 5 после m — 4 — 5, что согласуется с теоремой Такенса.
 [29]

В начале 70 — х годов анализ Ландау и Хопфа был подвергнут критике в работе исследователей из Франции и Голландии Дэвида Рюэля и Флориса Такенса. По Рюэлю и Такенсу, странный аттрактор и есть математический образ турбулентного движения.
 [30]

Страницы:  

   1

   2

   3

   4

ФИЗИКО-МАТЕМАТИЧЕСКИЕ НАУКИ / PHYSICS AND MATHEMATICS

Крылова Е.Ю.1, Душаканова Н. 2, Папкова И.В. 3 (науч.рук.), Бабенкова Т.В. 4

‘Кандидат физико-математических наук, Саратовский государственный университет им. Н.Г. Чернышевского,

2 Студент,3, ^Кандидат физико-математических наук, доцент Саратовский государственный технический университет им.

Гагарина Ю.А.

О ВЛИЯНИЕ ВНЕШНЕГО ШУМА НА СЦЕНАРИИ РЮЭЛЯ-ТАКЕНСА-НЬЮХАУЗА В БАЛКАХ ТИМОШЕНКО

Аннотация

Работа посвящена анализу влияния внешнего шума на параметрические колебания динамических систем. Показано, что с помощью внешнего воздействия можно управлять характерам их колебаний.

Ключевые слова: нелинейная динамика, индуцированные шумом переходы, параметрические колебания.

Krylova E.Y ‘, Dyshakanova N. 2, Papkova I.V. 3, Babenkova T.B. 4 ‘PhD in Physics and mathematics, Saratov State University, 2Student, 3,4 PhD in Physics and mathematics, assosiate professor, Saratov

State Technical University

ABOUT INFLUENCE OF EXTERNAL NOISE ON THE SCENARIO RUELLE-TAKENS-NEWHOUSE IN TIMOSHENKO

BEAM

Abstract

The purpose of work is analysis of external noise influences on the parametric oscillations of dynamical systems.

Keywords: nonlinear dynamics, noise-induced transitions, parametric oscillations.

В работе рассматривается влияние аддитивного внешнего шума на характер параметрических колебаний гибкой упругой балки модели Тимошенко. В таких областях как физика, химия, биология, уже показано, что случайные воздействия играют весьма существенную роль в поведении динамических систем [1]. Внешние шумы способны приводить не только к флуктуациям в характеристиках динамических систем, но и вызывать качественную перестройку их режимов.

ТУ 2

Рассматривается однослойная, упругая, изотропная балка, как область пространства л в декартовой системе координат XOZ (ось OX направлена слева направо вдоль срединной линии балки, ось OZ — вниз, перпендикулярно оси OX). Под срединной линией балки понимается фиксированная линия приведения z = 0. В указанной системе координат область, занимаемая балкой

определяется в виде

. Q = {х е [0, a ] — h < z < h} 2h _

a

длина балки. Балка находится под действием поперечной

q = q0( x)sin(o t) q on

знакопеременной нагрузки р , приложенной к некоторой области балки, где 0 и р амплитуда и частота

нагрузки соответственно.

Математическая модель нелинейных диссипативных колебаний балки строится на основе гипотезы Тимошенко [2], с учетом нелинейной зависимости между деформациями и перемещениями в форме Кармана [3]. К уравнениям движения элемента балки присоединяются граничные условия шарнирного опирания и нулевые начальные условия. Дифференциальная задача приводится к системе обыкновенных дифференциальных уравнений по пространственной координате методом конечных разностей (МКР) с

O(h2)

погрешностью , которая по времени решается методом Рунге-Кутта четвертого порядка точности. Применение МКР

позволяет рассматривать балку, как механическую систему с потенциально бесконечным числом степеней свободы. Аддитивный шум добавлен в систему в форме случайного слагаемого с постоянной интенсивностью

p = p (2.0 * rand()/(RAND MAX +1.0)-1.0) pn0 „ „ „

x n x n0 _ , где n0 — интенсивность шума. При исследовании колебаний

результаты, полученные для центральной точки срединной линии балки, обобщаются на всю балку. При получении численных

X = a/(2h) = 50

результатов использовались следующие параметры. коэффициент диссипации среды; n = 40 — число разбиений отрезка Х е [0;1]

— отношение линейных размеров балки,

S = 1

в МКР;

At = 39,0625-10″

методе Рунге-Кутты,

t е [0;2348]

— шаг по времени в

О = 5.3

При частоте нормальной нагрузки p был получен сценарий Рюэля-Такенса-Ньюхауса. Далее проводился анализ

влияния интенсивности аддитивного шума на характер колебаний балки.

Разрушения сценария Рюэля-Такенса-Ньюхауса обнаружено не было.

p < 1000

В числебнных экспериментах с интенсивностью аддитивного шума менее 1000 ( n0 ) отмечалось, что при

отношении амплитуды нормальной нагрузки к интенсивности шума более чем в 2 раз (q0 / pn0 2

) происходит снижение

реакции системы на шум. В случае

p n0 = 10

? при iiuvuuiiiiviLm:! uj

о /2

Фурье стал очищаться в области частот больших р . При 0

при превышении амплитудой внешней нагрузки значение 50 спектр мощности °p /2 = 500

шумовая составляющая на спектре осталась только в

q0 =1500

идентичны. В случае интенсивности шума pn0

области низких частот. При идентичны. В случае интенси

q0 > 700 q0 > 5000

спектр с учетом внешних флуктуаций и спектр без учета шумовой составляющей

pn0 = 100

n0 хаотическая реакция системы на внешний шум стала сокращаться при

при

шумовых составляющих в спектре Фурье почти не осталось. pn0 > 1000

Спектры мощность Фурье были серьезно зашумлены по всему ). Наблюдалось незначительное снижение реакции

В численных экспериментах с

q0 е [10,15000]

рассматриваемому интервалу амплитуд внешней нагрузки ( 0 на аддитивный внешний шум.

p = 5000

В численном эксперименте с интенсивностью внешнего шума n0 были обнаружены области, где система не только

не проявляла хаотических реакций на внешнее шумовое воздействие, но и под влиянием шумовой составляющей происходило

q0 =15000

уменьшение количества частот в спектре Фурье. Так, при 0 хаотические колебания под действием внешнего шума

перешли в квазипериодические (Таблица 1).

4

Полученные в результате численных экспериментов результаты позволяют сделать вывод о том, что с помощью внешнего воздействия можно управлять характером колебаний рассматриваемых распределенных механических систем.

Таблица 1

Амплитуда нормальной

q0

нагрузки, 0

p = 0

Интенсивность шума ^ п0

Интенсивность шума

Рп0 = 5000

q0 = 5000

q0 =15000

Литература

1. Хорстхемке В. Индуцированные шумом переходы: Теория и применение в физике, химии и биологии/ В. Хорстхемке, Р. Лефевр: Пер. с англ.-М.:Мир,1987.-400с.

2. Вольмир А.С. Нелинейная динамика пластинок и оболочек / А.С. Вольмир.- М.: Наука, 1972.- 492 с.

3. Kaiman, Th. Festigkeitsprobleme in Maschinenbau/ Th. Karman // Encykle. D. Math. Wiss. 1910. Vol. 4, №4, P. 311 — 385.

References

1. Horsthemke V. Inducirovannye shumom perehody: Teorija i primenenie v fizike, himii i biologii/ V. Horsthemke, R. Lefevr: Per. s angl.-M.:Mir,1987.-400s.

2. Vol’mir A.S. Nelinejnaja dinamika plastinok i obolochek / A.S. Vol’mir.- M.: Nauka, 1972.- 492 s.

3. Karman, Th. Festigkeitsprobleme in Maschinenbau/ Th. Karman // Encykle. D. Math. Wiss. 1910. Vol. 4, №4, P. 311 — 385.

Празян Т. Л.

Магистрант, физический факультет, ФГБОУ ВПО КемГУ, Россия, г. Кемерово Prazyan. tigran@yandex. ru

FOX-7: ПЕРВОПРИНЦИПНОЕ ИССЛЕДОВАНИЕ ВЫСОКОЭНЕРГЕТИЧЕСКИХ МАТЕРИАЛОВ

Аннотация

Целью настоящей работы является представление данных о структурном и электронном строении FOX-7 в газовой фазе, полученные различными ab initio методами.

iНе можете найти то, что вам нужно? Попробуйте сервис подбора литературы.

Ключевые слова: высокоэнергетические материалы, FOX-7, первопринципные методы.

Prazyan T. L.

Undergraduate student, Department of General Physics, Kemerovo State University, Russian Federation, Kemerovo FOX-7: AB INITIO STUDY OF THE HIGH ENERGY MATERIALS

Abstract

The aim of this work is to obtain data on the structural and electronic structure of FOX-7 in the gas phase obtained by different ab initio methods.

Keywords: high energy materials, FOX-7, ab initio methods.

Расчеты по оптимизации геометрии, расчету и анализу электронных свойств C2N4O4H4 (далее FOX-7) [1] проводились с использованием программного пакета CRYSTAL09 [2], основанный на методе линейной комбинации атомных орбиталей (ЛКАО). Базисные наборы [3], использовавшиеся при расчетах: C_6-21G*, H_3-1p1G, N_6-31d1G, O_6-31d1. В настоящей работе результаты приведены для FOX-7 в газовой фазе. Как было выяснено ранее, данная модель удовлетворительно описывает свойства изучаемых материалов и дает достаточно точные результаты в сравнении с экспериментальными данными.

На рис.1 (слева) показано молекулярное строение FOX-7. Как можно заметить, рассматриваемая молекула имеет две нитрогруппы и две аминогруппы, атомы кислорода и водорода которых отклонены от основной плоскости молекулы. Справа рис.1 представлена карта распределения электростатического потенциала для молекулы FOX-7. Видно, с аминогрупп вытекает заряд, на это указывают сплошные линии, а не нитрогруппы — натекает. Области отрицательного потенциала обозначены пунктирными линиями, положительного потенциала — сплошными линиями, поверхности нулевого потенциала — штрих-пунктирными линиями.

5

1