Конспект-сценарий урока математики в 5 классе
- Тема: Понятие обыкновенной дроби
- Цель: формировать понятие об обыкновенных дробях; способствовать развитию математической речи, оперативной памяти, произвольного внимания, наглядно-действенного мышления; воспитывать культуру поведения при фронтальной и индивидуальной формах работы.
- Учебные задачи, направленные на достижение личностных результатов обучения:
— формировать способность к самооценке на основе критерия успешности учебной деятельности;
- Учебные задачи, направленные на достижение метапредметных результатов обучения:
— формировать умения определять и формулировать цель на уроке с помощью учителя; проговаривать последовательность действий на уроке; работать по коллективно составленному плану; оценивать правильность выполнения действия; планировать своё действие в соответствии с поставленной задачей; вносить необходимые коррективы в действие после его завершения на основе его оценки и учета характера сделанных ошибок; высказывать своё предположение;
— формировать умение оформлять свои мысли в устной форме; слушать и понимать речь других; совместно договариваться о правилах поведения и общения в школе и следовать им.
- Учебные задачи, направленные на достижение предметных результатов обучения:
— формировать умения ориентироваться в своей системе знаний (отличать новое от уже известного с помощью учителя); добывать новые знания (находить ответы на вопросы, используя учебный текст учебника, свой жизненный опыт и информацию, полученную на уроке).
- Планируемые образовательные результаты:
Предметные: знать, что такое «доли», что показывает числитель дроби, знаменатель дроби; начать формирование умения решать задачи, содержание дроби.
Личностные: уметь осуществлять самооценку на основе критерия успешности учебной деятельности.
Метапредметные:
Регулятивные – уметь определять и формулировать цель на уроке с помощью учителя; проговаривать последовательность действий на уроке; работать по коллективно составленному плану; вносить необходимые коррективы в действие после его завершения на основе его оценки и учета характера сделанных ошибок; высказывать своё предположение.
Коммуникативные – уметь оформлять свои мысли в устной форме; слушать и понимать речь других; совместно договариваться о правилах поведения и общения в школе и следовать им.
Познавательные — умения ориентироваться в своей системе знаний (отличать новое от уже известного с помощью учителя); добывать новые знания (находить ответы на вопросы, используя учебный текст учебника, свой жизненный опыт и информацию, полученную на уроке); уметь извлекать из математических текстов необходимую информацию.
- Основные понятия: доля, дробь, числитель, знаменатель.
- Ресурсы:
- Учебник «Математика. 5 класс» (автор Мерзляк А.Г.);
- Презентация «Доли. Обыкновенные дроби»;
- Организация пространства: фронтальная, индивидуальная.
- Тип урока: урок открытия нового знания.
- Методы:
По источникам знаний: словесные, наглядные;
По степени взаимодействия учитель-ученик: эвристическая беседа;
Относительно дидактических задач: подготовка к восприятию;
Относительно характера познавательной деятельности: репродуктивный, частично-поисковый.
- Оборудование урока:
-проектор;
-экран;
-ноутбук.
- Организационный момент.
Эмоциональный настрой на урок.
Дети, вам тепло? (Да)
В классе светло? (Да)
Прозвенел уже звонок? (Да)
Уже закончился урок? (Нет)
Только начался урок? (Да)
Хотите учиться? (Да)
Значит можно всем садиться!
Обучающиеся садятся на свои места, включаются в деловой ритм урока
- Актуализация знаний.
- Мотивационная беседа.
— Света пришла после школы домой. На столе лежала записка, написанная мамой. В ней был написан список продуктов, которые надо было купить в магазине:
— 1 пакет молока;
— десяток яиц;
— 1 булку белого хлеба;
— половинку черного хлеба;
— четвертинку палки вареной колбасы.
— Света задумалась: «А четвертинка палки колбасы – это сколько? А половинка хлеба – это сколько?» Так задумавшись она шла по двору. Тут встретила подругу Наташу, которая, думала Света, знает про все на свете.
— Наташа, привет! Вот скажи – ты знаешь, что такое половинка хлеба и четвертинка палки вареной колбасы? – спросила Света.
— Нет, пока не знаю, но ты меня заинтересовала. Пойдем вместе к моему знакомому роботу Электронику и все узнаем. Он точно сможет нам помочь. – ответила Наташа.
И они отправились к роботу Электронику. Он жил на соседней улице. Он был на улице, гулял со своей собакой Ресси. Девочки подошли к нему.
— Здравствуй, Электроник. Смотри мама дала Свете список продуктов. А там какие – то непонятные половинка черного хлеба и четвертинка палки колбасы? Объясни нам, что это такое?
— Да, конечно, но давайте сначала устно порешаем. Это и поможет нам понять, что такое половинка хлеба и четвертинка палки колбасы. – сказал Электроник.
2. Устный счет
— Вам Электроник предлагает помочь Свете и Наташе и порешать вместе с ними.
168:24 = 7 (Д)
64:4 = 16 (Р)
9·9 = 81 (О)
5
3 S = (5·3 = 15 – Б)
3 V = (3·3·3 = 27 – ь)
— Давайте прочитаем. Что получилось? (Дробь)
— Света воскликнула: «А я знаю что такое дробь. Папа показывал дробь. Это такие маленькие шарики, которыми можно стрелять из ружья»
— Наташа сказала: «Я слышала как про барабанщика говорили, что он выбивает красивую дробь.»
— А кто еще нашел лексическое значение слова дробь? (Дробь — быстрое чередование ударов пальцами. )
— Вы правы, у слова дробь много значений. И кроме тех, о которых вы сказали, есть еще одно, которое связано с математикой.
- Изучение нового материала.
— Когда один предмет делят на несколько одинаковых частей, получаются дробные числа. А вот половинка хлеба и четвертинка палки колбасы – примеры дробных чисел. Именно такие примеры. Так половинка хлеба обозначает, что хлеб разделили на 2 равные части и взяли одну часть. А четвертинка палки колбасы обозначает, что палку колбасы разделили на 4 равные части и взяли одну часть.
— Света спросила: «Электроник, а как записывать такое числа? Ведь если я возьму 3 шоколадки, то я могу записать это цифрой. А как быть здесь?»
— Электроник сказал: «Они записываются так:
– хлеба
– палки колбасы
Читают так:
— Одна вторая хлеба.
— Одна четвертая палки колбасы.
Именно такие записи и называют обыкновенными дробями.
У каждой составляющей этой записи есть свое название.
Число, которое записано сверху – называется числителем дроби.
Линия, которая разделяет числа – называется чертой дроби.
Число, которое записано под чертой – называется знаменателем дроби.
Света спросила: «Электроник, а можно записать наоборот : 2 сверху, а 1 – снизу? Тогда двойка стала бы числителем, а единица — знаменателем»
Электроник ответил: «У числителя и знаменателя есть свои обязанности. Знаменатель дроби показывает. На сколько равных частей разделили что-то целое. А числитель показывает сколько частей взяли.»
— Давайте закрепим. Открываем учебник страница 173 № 675 (Прочитайте дроби. Назовите числитель и знаменатель каждой дроби и поясните, что обозначает.
Света сказала: «Теперь я поняла, мне нужно купить одну вторую хлеба и одну четвертую палку колбасы. Спасибо Электроник, спасибо ребята!»
- Физкултминутка
- Первичное закрепление нового материала.
— Мы попрощались с нашими героями и продолжаем работать дальше.
1. Математический диктант
— Решаем № 675. Проверим.
Кто сделал правильно, поставьте плюсик.
— Решаем № 676. Проверим.
Кто сделал правильно поставьте плюсик
- Решение задач
— Самостоятельное решение задач с проверкой № 680, 682
№680.
составляли яблони
— Кто решил правильно, поставьте плюсик.
№ 682
14+19 = 33 (с) – составляют 2 рассказа
(с) – составляет 1 рассказ
(с) – составляет 2 рассказ
— Кто решил правильно, поставьте плюсик.
- Домашнее задание. № 677, 679, 681.
- Рефлексия.
— На последующих уроках вы ещё очень многое узнаете про дроби, научитесь их складывать, вычитать, умножать и делить. А сегодня я бы хотела урок закончить притчей: (слайд)
Шел мудрец, а навстречу ему три человека, которые везли под горячим солнцем тележки с камнями для строительства. Мудрец остановился и задал вопрос каждому. У первого спросил: «А что ты делал целый день?». И тот с ухмылкой ответил, что целый день возил проклятые камни. У второго мудрец спросил: «А что ты делал целый день?», и тот ответил: «А я добросовестно выполнил свою работу». А третий улыбнулся, его лицо засветилось радостью и удовольствием: «А я принимал участие в строительстве храма!»
— Ребята! Давайте мы попробуем с вами оценить каждый свою работу за урок.
— Кто работал как первый человек?
— Кто работал добросовестно?
— Кто принимал участие в строительстве храма своих знаний?
Каждый из учащихся себя оценивает.
«Лист самооценки предметных достижений»
(выдается каждому ученику)
1. Моя задача (задание) заключалась в том, чтобы: ….
2. Я с заданием справился, / не справился.
3. Задание выполнено без ошибок (или есть такие-то недочёты): …
4. Задание выполнено самостоятельно (или с помощью (кого)…
5. Моя работа мной оценена так (слова-характеристики): превосходно, отлично, хорошо, нормально.
Оценка знаний учащихся
(Выдается каждому ученику)
Максимальный уровень (превосходно)
Решена новая, совершенно незнакомая задача.
Программный уровень (отлично)
Решена необычная, в чём-то новая задача.
Необходимый уровень (хорошо)
Знакомая задача решена полностью самостоятельно.
Необходимый уровень (нормально) Знакомая задача решена, но с ошибками или с чьей-то помощью.
Сценарий урока математики
в 5 классе
Составитель:
Потовиченко М.Н.,
учитель математики
МОУ «Шахтёрская СШ с.Грабово»
Тема урока: «В мире дробей» («Обыкновенные дроби»)
Тип урока: обобщение и систематизация изученного материала
Цель урока: Обобщить изученный материал по теме «Обыкновенные дроби» и уметь применять полученные знания при решении практических задач
Задачи:
Образовательные: обобщить и систематизировать знания учащихся об обыкновенных дробях; закрепить навык выделения целой части из дроби; сложения и вычитания дробей; решение задач на дроби; усилить практическую направленность обучения.
Развивающие: развивать у обучающихся умения сравнивать и обобщать, логически излагать мысли, развивать математический кругозор, мышление и речь, внимание и память.
Воспитательные: формировать устойчивую мотивацию и интерес к учению; учить ясно и точно выражать свои мысли; проводить рефлексию деятельности ребенка, развивать умения работать в паре.
Предметные: обобщить и систематизировать знания учащихся об обыкновенных дробях.
Личностные: формировать умения планировать свои действия в соответствии с учебным заданием; формировать умение работать в коллективе и находить согласованные решения; проявлять инициативу при выполнении заданий; осознать значимость обыкновенных дробей в практической жизни; ясно, точно, грамотно излагать свои мысли; исправлять и дополнять ответы других учащихся.
Метапредметные: видеть математическую задачу в окружающей жизни; самостоятельно определять цель своего обучения; осуществлять контроль своей деятельности по эталону; строить логические рассуждения.
Используемые формы организации познавательной деятельности учащихся: коллективная форма работы, парная, индивидуальная работа.
Оборудование и основные источники информации: компьютер, проектор, презентация к уроку, раздаточный материал (листы с заданиями, карточки с задачами).
Ход урока
I. Организационный момент.
Учитель:
— Здравствуйте, ребята. Рада вас видеть на сегодняшнем уроке.
Прозвенел звонок веселый.
Мы начать урок готовы.
Будем слушать, рассуждать,
И друг другу помогать.
Проверка домашнего задания.
Учитель:
— Прежде чем перейти к теме урока, поднимите руки те из вас, у кого есть вопросы по домашнему заданию. (Поднимают руки, те из учащихся, у кого есть вопросы).
— Если вопросов нет, то продолжим наш урок.
II. Мотивационный этап.
— Сегодня на уроке нам с вами предстоит выполнить большую и интересную работу. Мы отправимся в путешествие по волнам знаний. Сегодня вы покажете все свои умения и навыки, преодолевая препятствия и решая различные задания.
III. Постановка цели и задач урока.
Учитель:
Все готовы, и мы можем отправиться в наше плавание. А куда мы поплывем? Для ответа на этот вопрос расшифруем название острова.
Задание 1. Перед вами ребус. Отгадайте его.

— Итак, тема нашего урока «В мире дробей».
— А как вы думаете, исходя из темы нашего урока, какова цель нашего путешествия, к чему мы стремимся? (Наша цель: обобщить изученный материал по теме «Обыкновенные дроби» и уметь применять полученные знания при решении практических задач ).
— А что мы знаем о дробях? (У дроби есть числитель и знаменатель. Дроби можно складывать, вычитать, умножать и делить).
IV. Актуализация знаний.
Учитель:
— Давайте разберемся, почему дроби «разные»? Что такое дробь? А какие дроби вы знаете? (Правильные, неправильные).
— Объясните, какая дробь называется правильной, а какая неправильной. Приведите примеры. (Дети отвечают)
Задание 1. Устная работа. Прием «Хлопушка» (хлопок на неправильную дробь). Учитель по очереди называет дроби, когда учащиеся слышат неправильную дробь, они хлопают в ладоши.
;
;
;
;
;
;
;
;
;
;
;
— Все верно! Теперь я вижу, что ваши корабли наполнены знаниями, а это значит, что мы с вами можем уверенно продолжать наше плавание. Попутного ветра!
V. Решение практических задач.
Учитель:
— Посмотрим на карту нашего путешествия. И вот первый остров на нашем пути. Но для того, чтобы к нему добраться, нужен корабль.
1. Задание «Кораблики»
Карточки с числами: ;
;
;
;
;
;
Задание: неправильные дроби записать в виде смешанного числа, а смешанное число в виде неправильной дроби. Составить кораблик, у которого на борту показан знаменатель, парус – числитель, целое число расположить на флажке. (взаимопроверка с помощью слайда)
На выполнение задания отводится 5 мин.

Учитель:
— Выполняя разные задания на уроках, вам приходилось сравнивать дроби между собой. А какие правила сравнения дробей вы знаете? (Учащиеся формулируют правила). Итак, вам предстоит задание сравнить дроби.

Учитель:
— Молодцы! Мы выбрали правильный маршрут и не сбились с пути.
— Прямо по курсу остров «Посчитай-ка», но добраться до него не просто, нужно преодолеть подводные камни. Для этого вам предстоит выполнить следующее задание.
2. Задание. Выполните действия с дробями.
На выполнение задания отводится 5 минут.
Ребята выполняют вычисления. Проверка правильности выполненных заданий с помощью сигнальных карточек «Да» и «Нет».
3. Физминутка
Учитель:
— В пути немало трудностей мы преодолевали и немножечко устали. Ну, ребята, улыбнитесь и немного подтянитесь. Посмотрите влево, вправо, повращайте головой, разомните кисти рук, чтобы легок был наш путь.
4. Сокращение дробей
Учитель:
— Приглядитесь, там мерцает остров вдалеке. Давайте сократим путь и доберемся до него через пролив. Но для этого нам нужно вспомнить, как сокращать дроби. Ну что, вперед!
Сократите дроби:
-
; 2)
; 3)
; 4)
.
5. Задание «Подумай-ка»
Учитель:
— Этот остров на карте раньше никто не исследовал, поэтому он и называется «Неизвестный». Вам предстоит его открытие. А для этого придется проникнуть в его тайны и разгадать его загадки.
Задание. Определите, какая часть фигуры закрашена.
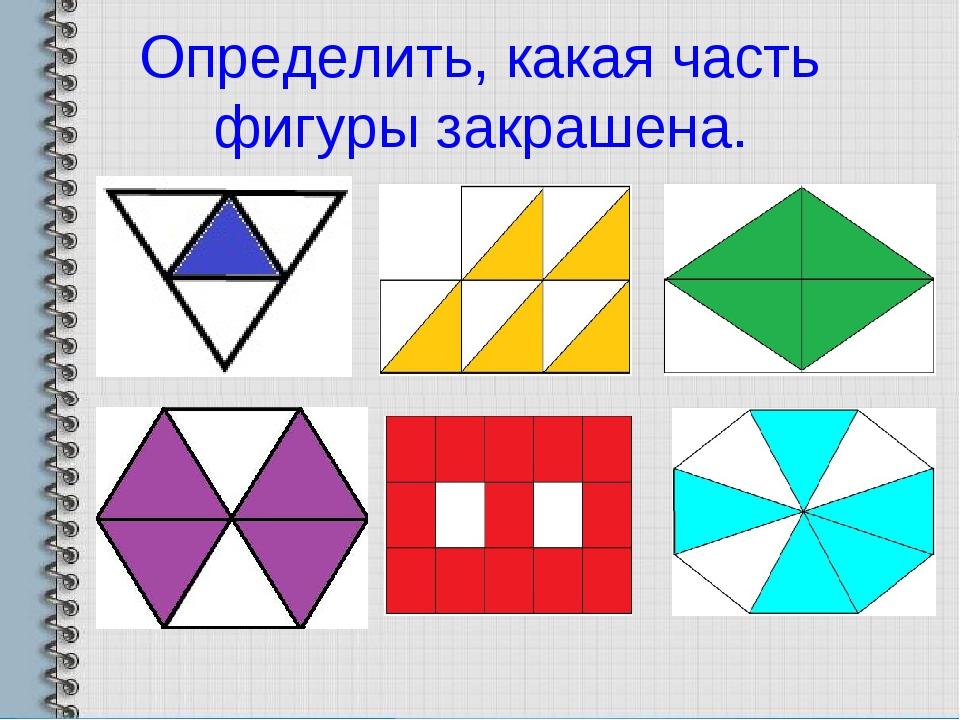
6. Решение задач.
Учитель:
— Мы почти достигли цели нашего плавания, и нам осталось проверить наши знания на практике. Для этого решим несколько задач.
-
Почтальону Печкину надо доставить 24 письма. Он уже доставил
всех писем. Сколько ему ещё осталось доставить? (15 писем)
-
Суточная норма витамина Е составляет 15 мг, это только
суточной нормы витамина С. Сколько мг витамина С необходимо употреблять в сутки? (60мг)
VI. Домашнее задание:
Составить кроссворд по теме «Обыкновенные дроби»
VII. Рефлексия.
Учитель:
Вот и закончилось наше путешествие. Я надеюсь, что сегодняшний урок был для вас интересен и поучителен. А закончить урок я хотела бы словами великого писателя Л.Н.Толстого: «Человек подобен дроби: в знаменателе – то, что он о себе думает, в числителе – то, что он есть на самом деле. Чем больше знаменатель, тем меньше дробь».
– Спасибо всем за урок!
Использованная литература:
-
Бунимович Е.А. Математика. Арифметика. Геометрия. 5 класс: учебник для общеобразовательных учреждений./ Е.А. Бунимович, Г.В. Дорофеев, С.Б.Суворова и др. – М.: Просвещение, 2010.
-
Гусев А.А. Математический кружок, 6 класс. – М., 2014
-
Лиман М.М. Школьникам о математике и математиках. – М., 1981
-
Олимпиадные задачи по математике. 5-6 кл. / сост. Ю.В.Лепёхин. – Волгоград, 2010.
Тема: «Обыкновенные дроби».
Задачи:
- обобщить и систематизировать знания об
обыкновенных дробях; - повысить уровень математического развития
обучающихся и расширить их кругозор; - развить у обучающихся интерес к занятиям
математикой; - углубить представление обучающихся об
использовании сведений из математики в
повседневной жизни; - воспитывать волю, упорство в достижении цели.
- содействовать воспитанию культуры общения
через работу в группах.
Учебно-методическое обеспечение:
Математика: Учеб. для 5 кл. общеобразоват.
учреждений/ Н.Я. Виленкин, В.И. Жохов, А.С. Чесноков,
С.И. Шварцбурд. – М.: Мнемозина, 2008.
Время реализации занятия – 80 минут.
Тип урока: урок обобщения и
систематизации знаний, умений, навыков.
Метод обучения: поисковый, словесный,
практический, использование некоторых методов и
приемов технологии развития критического
мышления.
Авторский медиапродукт – наглядная
презентация (операционная среда Windows XP, редактор
Microsoft Power Point)
Медиапродукт:
I. Среда: программа для создания презентаций
Microsoft PowerPoint, текстовый редактор Microsoft Word.
Вид медиапродукта: наглядная презентация
учебного материала
II. Структура презентации:
| № п/п |
СТРУКТУРНЫЕ ЭЛЕМЕНТЫ |
Временная реализация | № Слайда |
| 1 | Организационный момент. | 2 мин. | |
| 2 | Вступление. | 3 мин. | № 2-3 |
| 3 | Повторение материала прошлых уроков (работа в группах) |
30 мин. | №7-20 |
| 4 | Устные упражнения. | 5 мин. | №28-29 |
| 5 | Конкурс капитанов. | 5 мин. | №4-6 |
| 6 | Выступления обучающихся (сообщения). | 12 мин. | №25-26 |
| 7 | Работа с классом. | 10 мин. | №21-24 |
| 8 | Подведение итогов игры, награждение. | 5 мин. | |
| 9 | Рефлексия. | 4 мин. | №31. |
III. Схема взаимосвязи кадров презентации:
Взаимосвязь других кадров презентации
аналогична.
IV. Содержание кадров:
1. Титульный лист.
2. Вхождение в тему.
3. Выбери цифру.
4. Конкурс капитанов.
5-6. Задания для конкурса капитанов.
7-11. Занимательные задачи.
12-13. Расшифруй ребус.
14-20. Решение задач на отработку действий с
обыкновенными дробями.
21-24. Кому принадлежат данные слова?
25-26. Исторические сведения.
27-29. Отвечай, не робей, дай ответ поскорей!
30. Вы выиграли приз!
31. Подведение итогов. Рефлексия.
Целесообразность использования
медиапродукта на занятии:
- повышение эффективности усвоения учебного
материала за счет одновременного изложения
учителем необходимых сведений и показа
демонстрационных фрагментов; - эффективность индивидуального подхода к работе
учащихся на данном этапе урока (продуктивная
самостоятельная творческая деятельность,
развитие способностей, индивидуальная
траектория освоения материала, индивидуальное
время освоения, уровневая дифференциация)
Необходимое оборудование и материалы для
занятия – компьютер, проектор, спички,
сообщения обучающихся, сладкий приз.
Оформление аудитории: «Если вы хотите
участвовать в большой жизни, то наполняйте свою
голову математикой, пока есть к тому возможность.
Она окажет вам потом огромную помощь во всей
вашей работе» (М.И.Калинин)
План занятия
| № | Структурные элементы | Деятельность учителя | Деятельность учащихся | Время |
| 1 | Организационный момент | Проверка готовности к уроку. Мотивация учащихся. |
Положительный настрой на урок. | 2 |
| 2 | Целевая установка | Определение темы и целей работы на уроке. |
Восприятие | 3 |
| 3 | Актуализация знаний | Проверка знаний учащихся, полученных ранее. | Устное и письменное решение задач, работа с текстом |
30 |
| 4 | Физминутка. | Направлена на сохранение здоровья детей. | 2 | |
| 5 | Решение проблемных вопросов | Организация групповой работы по открытию новых знаний. |
Групповая работа. | 30 |
| 6 | Итог урока. Рефлексия. | Анализирует, подводит итоги. | Дают оценку своей работы на уроке. | 5 |
Карта занятия.
|
Комментарий хода урока |
Время (мин) | Слайд |
Развитие личностных |
|
| Репродуктивные формы деятельности | Продуктивные формы деятельности | |||
| Оргмомент. Проверка готовности к уроку, объединение в группы. Мотивация учащихся. Положительный настрой на урок. |
1 | Внимание | организованность, аккуратность |
|
| Вхождение в тему. Детям предлагается небольшое стихотворение, в основу которого заложена тема урока. Ребята определяют тему урока. |
2 | 2 | Внимание | рефлексивность, самостоятельность, мышление |
| Стадия вызова. Команды по очереди называют любую цифру, записанную на прямоугольнике. Под каждой цифрой скрыто задание. Командам даётся время на обсуждение вопроса. |
3 | Внимание, память | самостоятельность, системность, аргументированность, ясность речи, активность, культура эмоций, коммуникативная культура |
|
| Выбрав цифру 1, ребята попадают на этап «Занимательные задачи», где им будет предложено решить 4 задания. Получает балл та команда, которая первой даст правильный ответ. |
12 | 8-11 | Внимание, память, мышление | самостоятельность, коммуникативная культура |
| Выбрав цифру 2, ребята попадают на этап «Исторические сведения», на котором они узнают, что дроби встречаются не только в математике, но и в других сферах деятельности человека, например, в музыке. Здесь же предлагается заслушать сообщения обучающихся. |
10 | 25, 26 | Внимание, самостоятель-ность | аргументированность, ясность речи, активность, коммуникативная культура, культура эмоций, умение слушать |
| Задание под цифрой 3 – расшифровать ребус. Работают все команды, баллы начисляются по очерёдности выполнения работы. |
5 | 13 | Память | дисциплина, точность |
| На 4 этапе учитель предлагает ознакомиться с высказываниями великих людей и определить, кому принадлежат данные слова. |
5 | 22-24 | аргументированность, мышление |
|
| Физминутка. Направлена на сохранение здоровья детей. |
1 | Внимание Память |
||
| Выбрав цифру 5, ребята попадают на этап «Конкурс капитанов», где они проявят находчивость и смекалку. При затруднении возможна помощь команд. |
5 | 4-6 | Внимание, память |
рефлексивность, аргументированность, ясность речи, активность, организованность, самостоятельность |
| В конкурсе «Числа правят миром», зашифрованным под цифрой 6, нужно показать знания при работе с обыкновенными дробями. |
10 | 14-17, 20 | Внимание, память, мышление | ответственность, рефлексивность, самостоятельность |
| Под цифрой 7 предложены устные задания на повторение. Вопросы задаются каждой команде по очереди. |
7 | 28, 29 | Внимание, память | точность и ясность речи, активность |
| Большим подарком для детей будет приз, который спрятан под цифрой 8. |
1 | 30 | Дисциплина | культура эмоций |
| В заключение урока учитель предлагает определить ценность урока, его полезность, проводит рефлексию, предлагая детям оценить свою деятельность на уроке |
3 | 31 | Дисциплина, внимание. | рефлексивность, аргументированность, ясность речи |
ХОД УРОКА
1. Организационный момент (1 мин.)
Учитель: Сегодня у нас необычное
повторение темы «Обыкновенные дроби».
Необычность урока состоит в том, что это будет
урок – игра, где вам предстоит пройти несколько
этапов, на которых вы будете решать
математические и логические задачи. Для этого
вам потребуются знания и умения работать с
обыкновенными дробями, смекалка и быстрота
реакции. Познакомлю вас с правилами игры. Вот они.
Это игра, в которой каждой команде
предоставляется право выбора любого вопроса,
скрытого под цифрами на прямоугольнике. Команды
игроков одновременно отвечают на один и тот же
вопрос, причём правильно ответивший первым,
лишает соперника возможности ответить на этот же
вопрос. Вопрос одного раунда оценивается в одно
очко. Бывает, что ответ той или иной команды
максимально близок к правильному. Преподаватель
выносит окончательное решение: признать ответ
правильным или нет. Побеждает команда, набравшая
наибольшее количество очков. Готовы? Тогда мы
начинаем.
Приложение. Слайд 2
Есть такая дробь у нас,
Про неё пойдёт весь сказ.
Она из чисел состоит,
А меж ними, как мосточек,
Дробная черта лежит.
Над чертой – числитель, знайте,
Под чертою – знаменатель.
Дробь такую непременно
Надо звать обыкновенной.
Приложение. Слайд 3.
Командам по очереди предлагается назвать
любую цифру, записанную на прямоугольнике.
Задание, скрытое под цифрой 1 – «Занимательные
задачи» (Приложение.
Слайд 7)
Приложение. Слайд 8.
Задача 1: Коля закопал свой дневник на
глубину 5 метров, а Толя закопал свой дневник на
глубину 12 метров. Археологи далёкого будущего
когда–нибудь раскопают оба окаменевших
дневника с большим количеством окаменевших
двоек. В Колином дневнике они найдут 224 двойки, а в
Толином – четвёртую часть этих двоек. Сколько
всего окаменевших двоек найдут археологи в двух
дневниках?
Приложение. Слайд 9.
Задача 2: Один дедушка охотился в кухне на
тараканов и убил 15, а ранил 2/5 от числа убитых.
Половину тараканов дедушка ранил смертельно, и
они погибли от ран. А остальные раненые тараканы
выздоровели, но обиделись на дедушку, и ушли к
соседям навсегда. Сколько тараканов ушло к
соседям навсегда?
Приложение. Слайд 10.
Задача 3: Апельсин, состоящий из некоторого
количества равных долек, можно честно разделить
на 5 частей и съесть всем вместе. Тогда каждому
достанется по 3 дольки. А можно спрятаться в шкаф
и быстро слопать весь апельсин в одиночестве.
Сколько долек достанется тебе одному?
Приложение. Слайд 11.
Задача 4: Двадцать две девочки, гуляя в лесу,
нашли 88 грибов, а потом половина девочек
потерялась. Во сколько раз количество найденных
в лесу грибов больше, чем количество
потерявшихся там же девочек?
Задание, скрытое под цифрой 2 – «Исторические
сведения» (Приложение.
слайд 25)
Дроби можно встретить не только в математике,
но и в жизни. Примером этому служит Приложение, слайд 26 – «Дроби
в музыке». После этого учитель предлагает
заслушать по одному из участников от каждой
команды, которые подготовили небольшие
сообщения о том, где ещё можно встретить дроби,
кроме математики.
Задание, скрытое под цифрой 3 – «Расшифруй ребус»
(Приложение. Слайд 12)
Обучающимся предлагается составить слово,
используя первые буквы ответов.
Приложение. Слайд 13
- Название закона, расставляющего скобки.
- Название числа 3 для уравнения x + 2 = 5.
- Царица математики.
- a/в, название «в»
- x3, другое название степени.
- Первая буква алфавита. Ответ: сказка
Задание, скрытое под цифрой 4 – «Кому
принадлежат данные слова?» (слайд 21)
Приложение. Слайд 22.
Задание 1: Перед вами портреты великих
людей: Цицерона, Евклида и Эйлера. Кто из них
является автором строк: «Без знаний дробей никто
не может признаваться знающим арифметику»
Ответ 1. Цицерон Марк Туллий, римский
политический деятель, оратор и писатель.
Сторонник республиканского строя. Из сочинений
сохранились58 судебных и политических речей, 19
трактатов по риторике, политике, философии и
более 800 писем. Сочинения Цицерона – источник
сведений об эпохе гражданских войн в Риме.
Приложение. Cлайд 23.
Задание 2: У кого сохранилась поговорка
«Попасть в дроби означает попасть в трудное
положение» Ответ 2. У немцев.
Приложение. Слайд 24.
Задание 3: Кто из этих знаменитых людей, чьи
фамилии вы видите на слайде, сделал интересное и
меткое «арифметическое» сравнение, что человек
подобен дроби, числитель которой есть то, что
человек представляет собой, а знаменатель – то,
что он думает о себе. Чем большего мнения о себе
человек, тем больше знаменатель, а значит, тем
меньше дробь. Ответ 1. Л.Н. Толстой
Великий русский писатель Лев Николаевич Толстой
проявлял особый интерес к математике и её
преподаванию, много лет преподавал начала
математики в основанной им же Яснополянской
школе и написал оригинальный учебник
«Арифметики».
Задание, скрытое под цифрой 5 – «Конкурс
капитанов» (Приложение.
слайд 4)
Очередной конкурс начинаем,
Капитанов приглашаем.
Будут трудные задачи,
Пожелаем им удачи!
Приложение. Слайд 5. Задание
1: Разделить торт на 8 частей.
Проведя один разрез, получим 2 части, два
разреза – 4 части, три разреза – 6 частей. А как
разрезать торт на 8 частей тремя прямолинейными
разрезами?
Ответ: Одним разрезом делим торт на 2 коржа.
Двумя другими разрезами делим каждый корж на 4
части.
Приложение. Слайд 6.
Задание 2: Переложить спичку так, чтобы из
дроби 1/7 вышла 1/3.
Ответ:
Задание, скрытое под цифрой 6 – «Числа правят
миром»
Приложение. Слайд 14.
Где ни будешь, хоть за партой, хоть на даче,
Не ленись, трудись, учись решать задачи.
Приложение. Слайд 15.
Задача 1: Коробка из под конфет имеет форму
прямоугольного параллелепипеда. Её длина равна 28
см, ширина составляет длины, а высота –
ширины. Найдите объём
коробки.
Приложение. Слайд 16.
Задача 2: Длина прямоугольника м, ширина на
м. больше длины.
Найдите периметр прямоугольника.
Приложение. Слайд 17.
Задача 3: Прямоугольник разделили на 8 равных
частей. Закрасили сначала прямоугольника, потом
, потом
. Весь ли прямоугольник закрасили?
Приложение. Слайд 20.
Задача 4: Сложите числа 64 и
числа 18.
Задание, скрытое под цифрой 7 – «Отвечай, не
робей, дай ответ поскорей!» (Приложение,
слайды 27-28)
- Сколько минут в половине часа?
- Сколько граммов в половине килограмма?
- Сколько часов в одной трети суток?
- Сколько килограммов в четверти тонны?
- Сколько копеек составляет
рубля?
- От мотка телефонного провода длиной 12 м.
отрезали его четвёртую часть. Сколько метров
провода осталось в мотке? - Какую часть отрезка АВ составляет отрезок АD? (по
рисунку)
Приложение. Слайд 29. Задание
1: Какая часть окружности закрашена? (по
рисунку)
Задание 2: Площадь прямоугольника
равна 56м2. Сколько м2 площади будет
закрашено, если закрасить: а) одну клеточку; б) 2
клеточки; в) 3 клеточки; г) 4 клеточки; д) 5 клеточек?
Задание, скрытое под цифрой 8 – «Приз!»
(Приложение, слайд 30)
Команде, назвавшей данную цифру, вручается
сладкий приз.
Учитель: Вот и подошла к концу наша
игра. Каждый из вас, и победитель, и побеждённый
сегодня получит приз – хорошую оценку. Потому,
что все вы размышляли, решали и рассуждали. Может
быть не совсем правильно, но зато сами, а это
самое главное. Каждого из вас я попрошу оценить
свою работу на уроке (появляется слайд 31, Приложение). Если вы
получили удовольствие от урока, выбираете фигуру
1.Если вы считаете, что поработали сегодня
нормально, выберите фигуру 2. А если вы остались
недовольны своей работой, выберите фигуру 3.
Литература:
- Никольский С.М., Потапов М.К., Решетников Н.Н.,
Шевкин А.В. Арифметика. Пособие для
самообразования. – М.: Наука. Гл. ред. физ.-мат.
лит., 1988. - Совайленко В.К. Система обучения
математике в 5-6 классах: Кн. для учителя: Из опыта
работы. – М.: Просвещение, 1991. - Кузьминых Л.А. Математика в стихах. – Томск:
РЦРО, 2007. - Г. Остер «Занимательные задачи»
ПЛАН—КОНСПЕКТ УРОКА
«Понятие обыкновенные дроби»
(Тема урока)
Барсукова Светлана Николаевна
Тема и номер урока
в теме
«Понятие обыкновенные дроби»(1)
«Математика», А.Г.Мерзляк и др.,. Учебник для
учащихся 5класса общеобразовательных учреждений
«Вентана—Граф» , 2015г
8. Цель урока: открытие понятия обыкновенные дроби, учить читать, записывать
и понимать обыкновенные дроби.
9. Задачи:
— обучающие
— подвести учащихся к тому факту, что дроби напрямую связаны с понятием деления
— научить читать, записывать и понимать обыкновенные дроби.
—проконтролировать степень усвоения материала;
—развивающие: развитие познавательного интереса, расширение кругозора учащихся;
—воспитательные:
формирование коммуникативного опыта, опыта презентации полученных
результатов, оценка собственной деятельности.
10. Тип урока: урок открытия новых знаний
11. Формы работы учащихся: фронтальная, индивидуальная, парная
12. Необходимое техническое оборудование: компьютер, проектор.
13. Структура и ход урока
Таблица 1.
СТРУКТУРА И ХОД УРОКА
Название
используемых
ЭОР
(с указанием
порядкового
номера из
Таблицы 2)
Деятельность учителя
(с указанием действий с
ЭОР, например,
демонстрация)
Проверка готовности к
уроку
Самоопределение к
деятельности
Активизирует деятельность
учащихся по поиску
учебной проблемы,
помогает им сформировать
учебную проблему
Восприятие
информации,
наблюдения,
попытки
сформировать
проблему
Актуализация
опорных знаний
Подготовка мышления
детей:актуализацияЗУН,
тренировка
соответствующих
мыслительных операций
Учащиеся
включаются в
репродуктивную
деятельность,
предполагающую
выполнение
действий.
Учитель при объяснении
подводит учащихся к
новому изучаемому
материалу
Учащиеся
принимают участие
в изучении нового
материала
Включение в
систему знаний
Организация работы
учащихся на тренировку
полученных знаний
Устная работа по
полученному
материалу
Организация работы по
учебнику
Решение задач из
учебника № 693 –
Знакомство учащихся с
историей возникновения
дроби
Итог урока,
домашнее задание.
Подведение итогов
изученного, фронтальный
опрос
Отвечают на
вопросы. Запись
домашнего задания
Организация самооценки
учениками деятельности на
уроке
Приложение к плану—конспекту урока
«Понятие обыкновенные дроби»
(Тема урока)
Таблица 2.
ПЕРЕЧЕНЬ ИСПОЛЬЗУЕМЫХ НА ДАННОМ УРОКЕ ЭОР
Форма
предъявления
информации
(иллюстрация,
презентации),
Гиперссылка на ресурс,
обеспечивающий доступ к ЭОР
Включение в
систему
знаний
Закрепление
Обыкновенные
дроби
http://gotovimyrok.com/?page_id=25348
Приложение (сценарий урока)
ХОД УРОКА.
1.Организационное начало
Проверка готовности к уроку.
Ну—ка, проверь дружок,
Ты готов начать урок?
Всё ль на месте,
Всё ль в порядке,
Ручка, книжка и тетрадка?
Все ли правильно сидят?
Все ль внимательно глядят?
Каждый хочет получать
Только лишь оценку пять.
2.Постановка учебной цели.
. Объявление темы и обучающей цели урока. Тема сегодняшнего урока “Понятие
обыкновенные дроби”. Для этого на уроке вспомним и рассмотрим такие вопросы:
Слайд 2
1. Доля.
2. Половина, треть, четверть.
3. Обыкновенная дробь.
4. Что показывают числитель и знаменатель дроби.
3.Актуализация опорных знаний
Повторение изученного в начальных классах
Слайд 3
. Мама купила арбуз и разрезала его на несколько равных частей и дала по одной части
бабушке, папе, двум детям и себе. Посмотрите, на сколько частей мама разрезала арбуз. (Мама
разрезала на 5 частей, потому что в семье 5 человек, и чтобы арбуз достался каждому)
Кому первому мама дала арбуз и почему? (Мама первой дала арбуз бабушке, потому что она
старше и она женщина, затем она дала арбуз папе, а последнюю часть мама взяла себе, потому,
что тот, кто угощает кого—то, берёт самый последний)
Вспомним, что такое доля. Доля – каждая из равных частей единицы. Так как арбуз
разрезали на 5 равных частей, значит, его разделили на 5 долей и каждый получил “одну
пятую” долю арбуза, или, короче “одну пятую
Вспомним, как записывают доли.
Для записи любой доли используют горизонтальную чёрточку. Её называют дробной чертой.
Пишут: 1/5
Что показывает число под чертой? Число под чертой показывает, на сколько равных частей
(долей) разделили единицу.
Так как же образуются доли? (Когда предмет или единица измерения делятся на равные части)
Что показывает число под чертой? (Число под чертой показывает, на сколько равных долей
разделили целое)
Слайд 4
Самая известная из долей – это, конечно. Половина. Слова с приставкой “пол” можно услышать
часто: полчаса, полкилометра. Разделить целое на две равные части – половина. Долю ½
называют “половина”.
Название доли зависит от того, на сколько равных частей разделили единицу. Разделили на три
части — “треть”. Долю 1/3 называют “треть”.
Если целое разделить на 4 равные части, то получится ¼ или по—другому говорят “четверть”.
Скажите, когда мы говорим четверть? (Учебная четверть, четверть часа)
А как же называются другие доли?
Чтобы назвать доли пользуются словами “пятая”, “шестая”
Читаем доли.
Слайд 5. Прочитайте доли ; ; ; ; .
4. Работа по теме урока.
Слайд 6
Объяснение нового материала.
. Разгадайте ребус и узнаете, с чем мы сейчас познакомимся
• 1. 1/60 минуты – это 1 … .
• 2. Единица измерения площади.
• 3. Как по— другому можно назвать «равные части»?
• 4. Прямоугольный параллелепипед, у которого все измерения равны.
• 5. 20 минут – это … часа.
“Дробь”. Сегодня на уроке мы познакомимся с понятием обыкновенная дробь
Оказывается доли по— другому, называют?( дробями), а именно обыкновенными дробями
Записи вида 4/7 называют обыкновенными дробями… 4 — числитель дроби, 7 — знаменатель
дроби. Чтобы лучше запомнить, что такое числитель и что такое знаменатель прочитаете
стихотворение.
Каждый может за версту
Видеть дробную черту.
Над чертой – числитель, знайте,
Под чертою – знаменатель.
Дробь такую, непременно,
Надо звать обыкновенной.
5. Включение в систему знаний
Слайд 7
Назовите числитель и знаменатель каждой дроби. 2/5 (числитель 2, знаменатель 5),
6/11 (числитель 6, знаменатель 11), 5/9 (числитель 5, знаменатель 9), 7/35 (числитель 7,
знаменатель 35), 1/8 (числитель 1, знаменатель 8).
При чтении дробей надо помнить: числитель дроби – количественное числительное женского
рода (одна, две, восемь и т.д.), а знаменатель – порядковое числительное (седьмая, сотая, двести
тридцатая и т.д.)
Например: — одна пятая; — две шестых; — восемьдесят три сто пятьдесят вторых.
. Знаменатель показывает, на сколько долей(частей) делят, а числитель – сколько таких долей
(частей)взято.
Прочитайте дроби. Что показывает числитель и знаменатель каждой дроби?
6. Закрепление изученного.
А сейчас я буду называть дроби, а вы их будете записывать в тетради (один ученик работает на
переносной доске)
Две седьмых. Четыре девятых. Одна сотая. Шесть восьмых. Три двадцать пятых. Половина.
Проверьте, правильно вы записали дроби или нет (взаимопроверка, а затем по слайду , ,
, , , ). Обменяйтесь тетрадками и проверьте работу соседа
Слайд 8(проверка)
Слайд 9
Запишите с помощью дроби, какая часть фигуры закрашена (один ученик работает на доске, а
остальные в тетрадях)
Попробуйте выразить эту часть разными дробями
Работа в тетради № 693,стр.178
Прочитайте задание. Что нужно выполнить? (Нужно начертить координатный луч, единичный
отрезок которого 9 клеток и отметить на нем точки ,соответствующие дробям)
Математический диктант – слайд 10 (с последующей проверкой)
Имеются геометрические фигуры. Всего их 36.
составляют 1/6 всех фигур,
составляют 1/9 всех фигур,
составляют 1/12 всех фигур,
остальные фигуры — .
Сколько квадратов среди фигур?
7.ИСТОРИЧЕСКАЯ СПРАВКА
Как же появились дробные числа?
Не всегда результат измерения или стоимость товара удавалось выразить натуральным числом.
Так появились дроби. Сначала люди пользовались наиболее простыми дробями , ,
.Таким образом, к семье натуральных чисел присоединились дробные.
В русском языке слово дробь появилось в 8 веке, оно происходило от слова “дробить”
разбивать на части, ломать.
В первых учебниках математики 17 века дроби так и называли “ломаные” числа. Черта в записи
дроби стала использоваться около 300 лет назад.
В старину на Руси использовались монеты достоинством меньше одной копейки: грош —
копейки и полушка — копейки.
Интересная система дробей была в Древнем Риме. Она основывалась на делении на 12 долей
единицы веса, которая называлась асс.
А для дробей, получающихся путём раздробления двенадцатых долей на более мелкие, были
особые названия. Даже сейчас иногда говорят: “Он скрупулёзно изучил этот вопрос” это
значит, что вопрос изучен до конца. А происходит странное слово скрупулёзно от римского
названия асса – “скрупулус”.
8. Итог урока.
слайд 1
Что такое доля? (Доля – каждая из равных частей единицы)
Какие дроби называют обыкновенными? Приведите примеры обыкновенных дробей. (Записи
вида , называют обыкновенными дробями)
Как называется число, которое пишут над дробной чертой? Как называется число, которое
пишут под дробной чертой? (Число, которое записывают над чертой, называется числитель, под
чертой — знаменатель)
Что показывают числитель и знаменатель дроби? (Знаменатель показывает, на сколько частей
делят, а числитель – сколько таких частей взято)
Домашнее задание
— п.25 №675, № 678, №694. Выставление оценок.
10. РЕФЛЕКСИЯ.
У вас на партах кружки разного цвета. Зеленые кружки— да, тема усвоена. Красные – нет, тема
не усвоена. Желтые – недостаточно усвоена. Я прошу вас оценить усвоения материала с
помощью одного из кружков, поместив их на доске .
Конспект-сценарий урока математики в 5 классе
Тема: Понятие обыкновенной дроби
Цель: формировать понятие об обыкновенных дробях; способствовать развитию математической речи, оперативной памяти, произвольного внимания, наглядно-действенного мышления; воспитывать культуру поведения при фронтальной и индивидуальной формах работы.
Учебные задачи, направленные на достижение личностных результатов обучения:
— формировать способность к самооценке на основе критерия успешности учебной деятельности;
Учебные задачи, направленные на достижение метапредметных результатов обучения:
— формировать умения определять и формулировать цель на уроке с помощью учителя; проговаривать последовательность действий на уроке; работать по коллективно составленному плану; оценивать правильность выполнения действия; планировать своё действие в соответствии с поставленной задачей; вносить необходимые коррективы в действие после его завершения на основе его оценки и учета характера сделанных ошибок; высказывать своё предположение;
— формировать умение оформлять свои мысли в устной форме; слушать и понимать речь других; совместно договариваться о правилах поведения и общения в школе и следовать им.
Учебные задачи, направленные на достижение предметных результатов обучения:
— формировать умения ориентироваться в своей системе знаний (отличать новое от уже известного с помощью учителя); добывать новые знания (находить ответы на вопросы, используя учебный текст учебника, свой жизненный опыт и информацию, полученную на уроке).
Планируемые образовательные результаты:
Предметные: знать, что такое «доли», что показывает числитель дроби, знаменатель дроби; начать формирование умения решать задачи, содержание дроби.
Личностные: уметь осуществлять самооценку на основе критерия успешности учебной деятельности.
Метапредметные:
Регулятивные – уметь определять и формулировать цель на уроке с помощью учителя; проговаривать последовательность действий на уроке; работать по коллективно составленному плану; вносить необходимые коррективы в действие после его завершения на основе его оценки и учета характера сделанных ошибок; высказывать своё предположение.
Коммуникативные – уметь оформлять свои мысли в устной форме; слушать и понимать речь других; совместно договариваться о правилах поведения и общения в школе и следовать им.
Познавательные — умения ориентироваться в своей системе знаний (отличать новое от уже известного с помощью учителя); добывать новые знания (находить ответы на вопросы, используя учебный текст учебника, свой жизненный опыт и информацию, полученную на уроке); уметь извлекать из математических текстов необходимую информацию.
Основные понятия: доля, дробь, числитель, знаменатель.
Ресурсы:
Учебник «Математика. 5 класс» (автор Мерзляк А.Г.);
Презентация «Доли. Обыкновенные дроби»;
Организация пространства: фронтальная, индивидуальная.
Тип урока: урок открытия нового знания.
Методы:
По источникам знаний: словесные, наглядные; По степени взаимодействия учитель-ученик: эвристическая беседа; Относительно дидактических задач: подготовка к восприятию; Относительно характера познавательной деятельности: репродуктивный, частично-поисковый.
Оборудование урока:
-проектор;
-экран;
-ноутбук.
Организационный момент.
Эмоциональный настрой на урок.
Дети, вам тепло? (Да)
В классе светло? (Да)
Прозвенел уже звонок? (Да)
Уже закончился урок? (Нет)
Только начался урок? (Да)
Хотите учиться? (Да)
Значит можно всем садиться!
Обучающиеся садятся на свои места, включаются в деловой ритм урока
Актуализация знаний.
-
Мотивационная беседа.
- Понятие обыкновенной дроби
PPTX / 27.42 Мб
- Понятие обыкновенной дроби
— Света пришла после школы домой. На столе лежала записка, написанная мамой. В ней был написан список продуктов, которые надо было купить в магазине:
— 1 пакет молока;
— десяток яиц;
— 1 булку белого хлеба;
— половинку черного хлеба;
— четвертинку палки вареной колбасы.
— Света задумалась: «А четвертинка палки колбасы – это сколько? А половинка хлеба – это сколько?» Так задумавшись она шла по двору. Тут встретила подругу Наташу, которая, думала Света, знает про все на свете.
— Наташа, привет! Вот скажи – ты знаешь, что такое половинка хлеба и четвертинка палки вареной колбасы? – спросила Света.
— Нет, пока не знаю, но ты меня заинтересовала. Пойдем вместе к моему знакомому роботу Электронику и все узнаем. Он точно сможет нам помочь. – ответила Наташа.
И они отправились к роботу Электронику. Он жил на соседней улице. Он был на улице, гулял со своей собакой Ресси. Девочки подошли к нему.
— Здравствуй, Электроник. Смотри мама дала Свете список продуктов. А там какие – то непонятные половинка черного хлеба и четвертинка палки колбасы? Объясни нам, что это такое?
— Да, конечно, но давайте сначала устно порешаем. Это и поможет нам понять, что такое половинка хлеба и четвертинка палки колбасы. – сказал Электроник.
2. Устный счет
— Вам Электроник предлагает помочь Свете и Наташе и порешать вместе с ними.
168:24 = 7 (Д)
64:4 = 16 (Р)
9·9 = 81 (О)
5

3 V = (3·3·3 = 27 – ь)
— Давайте прочитаем. Что получилось? (Дробь)
— Света воскликнула: «А я знаю что такое дробь. Папа показывал дробь. Это такие маленькие шарики, которыми можно стрелять из ружья»
— Наташа сказала: «Я слышала как про барабанщика говорили, что он выбивает красивую дробь.»
— А кто еще нашел лексическое значение слова дробь? (Дробь — быстрое чередование ударов пальцами. )
— Вы правы, у слова дробь много значений. И кроме тех, о которых вы сказали, есть еще одно, которое связано с математикой.
Изучение нового материала.
— Когда один предмет делят на несколько одинаковых частей, получаются дробные числа. А вот половинка хлеба и четвертинка палки колбасы – примеры дробных чисел. Именно такие примеры. Так половинка хлеба обозначает, что хлеб разделили на 2 равные части и взяли одну часть. А четвертинка палки колбасы обозначает, что палку колбасы разделили на 4 равные части и взяли одну часть.
— Света спросила: «Электроник, а как записывать такое числа? Ведь если я возьму 3 шоколадки, то я могу записать это цифрой. А как быть здесь?»
— Электроник сказал: «Они записываются так:


Читают так:
— Одна вторая хлеба.
— Одна четвертая палки колбасы.
Именно такие записи и называют обыкновенными дробями.
У каждой составляющей этой записи есть свое название.
Число, которое записано сверху – называется числителем дроби.
Линия, которая разделяет числа – называется чертой дроби.
Число, которое записано под чертой – называется знаменателем дроби.
Света спросила: «Электроник, а можно записать наоборот : 2 сверху, а 1 – снизу? Тогда двойка стала бы числителем, а единица — знаменателем»
Электроник ответил: «У числителя и знаменателя есть свои обязанности. Знаменатель дроби показывает. На сколько равных частей разделили что-то целое. А числитель показывает сколько частей взяли.»
— Давайте закрепим. Открываем учебник страница 173 № 675 (Прочитайте дроби. Назовите числитель и знаменатель каждой дроби и поясните, что обозначает.
Света сказала: «Теперь я поняла, мне нужно купить одну вторую хлеба и одну четвертую палку колбасы. Спасибо Электроник, спасибо ребята!»
Физкултминутка
Первичное закрепление нового материала.
— Мы попрощались с нашими героями и продолжаем работать дальше.
1. Математический диктант
— Решаем № 675. Проверим.





Кто сделал правильно, поставьте плюсик.
— Решаем № 676. Проверим.



Кто сделал правильно поставьте плюсик
-
Решение задач
— Самостоятельное решение задач с проверкой № 680, 682
№680.

— Кто решил правильно, поставьте плюсик.
№ 682
14+19 = 33 (с) – составляют 2 рассказа


— Кто решил правильно, поставьте плюсик.
Домашнее задание. № 677, 679, 681.
Рефлексия.
— На последующих уроках вы ещё очень многое узнаете про дроби, научитесь их складывать, вычитать, умножать и делить. А сегодня я бы хотела урок закончить притчей: (слайд)
Шел мудрец, а навстречу ему три человека, которые везли под горячим солнцем тележки с камнями для строительства. Мудрец остановился и задал вопрос каждому. У первого спросил: «А что ты делал целый день?». И тот с ухмылкой ответил, что целый день возил проклятые камни. У второго мудрец спросил: «А что ты делал целый день?», и тот ответил: «А я добросовестно выполнил свою работу». А третий улыбнулся, его лицо засветилось радостью и удовольствием: «А я принимал участие в строительстве храма!»
— Ребята! Давайте мы попробуем с вами оценить каждый свою работу за урок.
— Кто работал как первый человек?
— Кто работал добросовестно?
— Кто принимал участие в строительстве храма своих знаний?
Каждый из учащихся себя оценивает.
«Лист самооценки предметных достижений»
(выдается каждому ученику)
1. Моя задача (задание) заключалась в том, чтобы: ….
2. Я с заданием справился, / не справился.
3. Задание выполнено без ошибок (или есть такие-то недочёты): …
4. Задание выполнено самостоятельно (или с помощью (кого)…
5. Моя работа мной оценена так (слова-характеристики): превосходно, отлично, хорошо, нормально.
Оценка знаний учащихся
(Выдается каждому ученику)
Максимальный уровень (превосходно)
Решена новая, совершенно незнакомая задача.
Программный уровень (отлично)
Решена необычная, в чём-то новая задача.
Необходимый уровень (хорошо)
Знакомая задача решена полностью самостоятельно.
Необходимый уровень (нормально) Знакомая задача решена, но с ошибками или с чьей-то помощью.
Сафина Л.Р.
МОБУ СОШ д.Большебадраково Бураевский район
Республики Башкортостан
учитель математики
Обыкновенные дроби
(урок открытия новых знаний)
Тип урока: «Открытие» нового знания
Основные цели: формировать умение записывать результат деления в виде дроби; формировать способность к построению алгоритма записи результата деления в виде дроби в буквенном виде.
Ход урока.
Организационный момент. Мотивационный этап.
Мама купила арбуз и разрезала его на 6 равных частей: бабушке, дедушке, папе, двум детям и себе.
Какая часть арбуза достанется каждому члену семьи?
Практическая часть. Устная работа.
Решите задачи
Сколько ушей у трёх мышей?
Сколько лап у двух медвежат?
У семи братьев по одной сестре. Сколько всего сестёр?
У бабушки Даши внучка Маша, кот Пушок и собака Дружок. Сколько всего внуков у бабушки?
Над рекой летели птицы: голубь, щука, 2 синицы, 2 стрижа и 5 угрей. Сколько птиц? Ответь скорей!
Горело 7 свечей. 2 свечи погасили. Сколько свечей осталось? (2. остальные сгорели)
В корзине три яблока. Как поделить их между тремя детьми так, чтобы одно яблоко осталось в корзине? ( отдать одно яблоко вместе с корзиной).
На берёзе три толстых ветки, на каждой толстой ветке по три тоненьких веточки. На каждой тоненькой веточке по одному яблочку. Сколько всего яблок? ( Нисколько — на берёзе яблоки не растут.)
Сообщение темы урока
Сегодня мы с вами познакомимся с обыкновенными дробями.
Подготовка к работе на основном этапе
Хорошо, когда на столе есть целое яблоко, и можно его съесть одному. Но иногда приходится делить яблоко на части, т.е. дробить, чтобы поделиться с кем-нибудь. Так получаются ДРОБИ.
Помните, как было в детском мультфильме:
«Мы делили апельсин,
Много нас, а он один…
Приведите свой жизненный пример деления одного целого предмета на части.
Интересно, а в древности знали про дроби ?
В древности к целым и дробным числам относились по-разному: предпочтения были на стороне целых чисел. «Если ты захочешь делить единицу, математики высмеют тебя и не позволят это делать», — писал основатель
афинской Академии Платон.
Но не все древнегреческие математики соглашались с Платоном. С дробями свободно обращались Архимед и Герон Александрийский
Даже Пифагор, который трепетно относился к натуральным числам, создавая теорию музыкальной шкалы, связал основные музыкальные интервалы с дробями
Каждый может за версту
Видеть дробную черту.
Над чертой – числитель, знайте,
Под чертою – знаменатель.
Дробь такую, непременно,
Надо звать обыкновенной.
Назовите числитель и знаменатель каждой дроби
В Древнем Китаевместо черты использовали точку
½ — «половина», «пол»
⅓ — «треть»
¼ — «четверть»
⅙ — «полтрети»
⅛ — «полчети»
⅟12 – «пол-полтрети»
Первым дробную черту ввёл итальянский математик Леонардо Пизанский (Фибоначчи)
в 1202 году
Физкультминутка
Видишь, бабочка летает, (Машем руками-крылышками.)
На лугу цветы считает (Считаем пальчиком).
— Раз, два, три, четыре, пять. (Хлопки в ладоши.)
Ох, считать не сосчитать! (Прыжки на месте.)
За день, за два и за месяц… (Шагаем на месте.)
Шесть, семь, восемь, девять, десять. (Хлопки в ладоши.)
Даже мудрая пчела (Машем руками-крылышками.)
Сосчитать бы не смогла! (Считаем пальчиком.)
Усвоение новых знаний и способов действий
Запишите в виде обыкновенной дроби
Две восьмых
Четыре двенадцатых
Одна тысячная
Шесть шестнадцатых
Три двадцать пятых
Четверть
Закрашенная часть каждой фигуры обозначена дробью .
Если дробь записана верно, то хлопайте;
если дробь записана неверно, то топайте.
Работа над задачей
1. Сколько часов с сутках?
2. Какая часть суток пройдет если часы будут показывать:
1) 7 часов утра; 2) 15 часов дня; 3) 20 часов вечера
2. Мама приготовила к обеду пирог и разделила его на 8 частей. За обедом каждый член семьи съел одно и то же количество кусочков. Сколько человек живет в семье? Какая часть пирога была съедена? Какая часть пирога осталась?
VIII. Рефлексия
Ответьте на вопрос задачи поставленной в начале урока. Какая часть арбуза досталась каждому члену семьи?
Выберите утверждение и поднимите смайлики
Домашнее задание
Вкусное задание:
1) Купи мандарин или апельсин.
Раздели его на дольки, посчитай, сколько
всего долек? Угости своих родных и не забудь записать, какую часть фрукта получил каждый, и какая часть досталась тебе.
2) Купи большую шоколадку.
Раздели её на дольки, посчитай,
сколько всего долек?
Угости своих родных и не забудь записать, какую часть шоколадки получил каждый, и какая часть досталась тебе.
Литература.
1.Н.А.Ким Поурочное планирование. Математика 5 кл., — Волгоград, Учитель, 2016.
2.А.В.Фарков Математические олимпиады. М., Экзамен, 2016
3.В.Н.Рудницкая Дидактические материалы по математике М., Экзамен, 2014
Интернет ресурсы:
• http://festival.1september.ru
• http://fcior.edu.ru
• http://www.metod-kopilka.ru





