Сценарий занятия математического кружка

Занятие математического кружка

Тема: «Точка. Прямая линия. Виды линий»

Ввести понятие точки, прямой ,кривой ,ломаной, замкнутой, незамкнутой, самопересекающейся линий и линий без самопересечений.

Повторить круг вопросов, связанный с темой «Множество».

Цели:

Образовательные: 

Ввести понятие точки, прямой ,кривой ,ломаной      замкнутой, незамкнутой, самопересекающейся линии и линии без самопересечений.

Повторить круг вопросов, связанный с темой «Множество».

Развивающие:

• развитие математической речи, памяти, навыков самостоятельной работы, правильной оценки своих способностей
• Формирование у учащихся представления о способах поиска информации, исследовательских и творческих качеств личности
• Развитие интереса к предмету, познавательной деятельности учащихся;
• умения наблюдать, сравнивать, обобщать;
• Развитие памяти, логического мышления, умения сравнивать и из общего выделять главное.

Воспитательные:

• воспитание активности и творческого отношения к работе на уроке,

дружелюбных отношений в множестве коллектива; умения оценить друг друга.

• Формирование внимательности, собранности, культуры речи.

     Ход занятия:

1. Организационный момент.
2. Разминка

          Решение логических задач.

1.В соревнованиях по бегу Ваня, Гриша и Дима заняли первые три места. Какое место занял каждый из ребят, если Гриша занял не второе и не третье место, а Дима – не третье.

2.Коля и Петя живут в соседних домах. Идя в школу, Коля вышел из дома одновременно с Петей, значит Петя вышел из дома …(одновременно с Колей).

3.Нина живёт к школе ближе, чем Вера, а Вера ближе, чем Зоя. Кто живёт ближе к школе – Нина или Зоя?

4.Если Андрей на 2 года старше Вани, а Ваня на 3 года старше Коли, то кто старше – Андрей или Коля – и на сколько лет?

1. Работа по теме занятия.

— Что изучает геометрия?

— Какие фигуры вы можете назвать?

—  А можете ли вы назвать самую простую геометрическую фигуру?

В русском языке слово «точка» — это знак препинания, «точка назначения» — это место на карте. Нас сегодня будет интересовать геометрический смысл слова «точка».

Точка – фигура, изображающая предмет, размерами которого можно пренебречь. Почему?

Итак, точка – самая маленькая геометрическая фигура. Но любой, даже самой маленькой фигуре, обычно дают имя. Как называют точки?

1. Изобразите две точки А и В. Поставьте точку С так, чтобы она была посередине между ними. Говорят, что точка С лежит между точками А и В. А если точка лежит не в середине – будет ли она лежать между точками А и В? Отметьте точки Д и Е так, чтобы Д была между точками А и С, Е между С и В.

Если мы будем непрерывно перемещать точку в каком-либо направлении, как вы думаете, что мы получим? Можно ли назвать линией след, который самолет оставляет в небе? Таким же образом, перемещая карандаш по бумаге, не отрывая, мы получим линию. Так что же такое линия? Дайте определение. Линия – геометрическая фигура, которая может быть получена при непрерывном перемещении точки.  

1. Поставь в тетради две точки, соедини их какой-нибудь линией. Сколькими линиями можно соединить эти точки? Если вы сделаете это по линейке, то получится прямая линия, если от руки, то получится кривая линия, а если соединить с помощью нескольких отрезков, не лежащих на прямой, то получится ломаная.
2. Геометрия живет вокруг нас. Легче всего увидеть линию в упавшей на пол веревке. В виде линии можно увидеть ствол дерева. Приведите примеры линий, которые вы видите вокруг себя.

Прямые и ломаные можно изображать с помощью линейки, а кривые линии с помощью линейки нарисовать нельзя. Некоторые кривые линии можно нарисовать с помощью лекала, некоторые с помощью циркуля. Какую кривую, известную вам, можно изобразить с помощью циркуля.

1. А — множество прямых и их частей, В – множество ломаных линий, С – множество кривых, Д – множество всех линий. Составьте диаграмму Венна.  

   

До сих пор мы изображали линии на доске и в тетради, при этом получали линии, которые укладываются в плоскости. Как можно назвать такие линии? Мы с вами знаем, что существуют фигуры, которые не укладываются в плоскости – пространственные. И линии тоже бывают пространственные. Проще всего изобразить пространственную линию на поверхности куба, пирамиды, шара, конуса (показать на модели). Будет ли пространственной линия, лежащая в одной грани куба?

Линии

                                      Плоские                   Пространственные

Примером пространственных линий могут служить перила винтовой лестницы, шнурки на ботинках. Приведите собственные примеры пространственных линий.

1. На листе бумаги нарисовали линию. После этого лист смяли. Верно ли, что линия осталась плоской? Можно ли на смятом листе найти плоскую линию (выполняют на заранее приготовленных листках)?

Рассмотрим  рис.1:

 Чем отличаются линии первой группы от линий второй группы?

Линии

                                         Замкнутые                   Незамкнутые

Дайте определение замкнутой и незамкнутой линии. Какие линии можно обводить несколько раз, не отрывая карандаш от бумаги (одним росчерком)? Существует секрет, с помощью которого можно определить, можно ли изобразить фигуру одним росчерком?

Обход фигуры возможен, если число нечетных узлов два или ни одного.   

Линии

                         Самопересекающиеся              Простые

Могут ли простые линии быть плоскими, кривыми, ломаными, пространственными. А самопересекающиеся? Сколько точек самопересечения может быть у линии? Может ли быть прямая с самопересечением?

1. Рассмотрим линии, изображённые на рис.2

 Выпишите : А-множество замкнутых кривых, В-множество замкнутых ломаных, С-множество незамкнутых кривых, Д-множество незамкнутых ломаных, Е-множество замкнутых линий, G-множество кривых линий, М-множество самопересекающихся линий.

4.Веселая минутка. Задачи – шутки.

1. Имеет 4 зуба. Каждый день появляется за столом, а ничего не ест. Что это?

2. На какое дерево садится ворона во время проливного дождя?

3. У бабушки Даши внучка Маша, кот Пушок, собака Дружок. Сколько у бабушки внуков?

4. Сколько горошин может войти в обыкновенный стакан?

5. На четырёх ногах стою, ходить же вовсе не могу.

1. Может ли дождь идти два дня подряд?

5.Самостоятельная работа (выполняется на изготовленных дома моделях пространственных фигур).

1. На своих моделях зеленым карандашом изобразите плоскую незамкнутую кривую с одной точкой самопересечения.
2. Синим карандашом пространственную замкнутую простую кривую.
3. Красным карандашом незамкнутую пространственную ломаную с двумя точками самопересечения.

1. Решение олимпиадных задач

      1.  Напишите подряд семь цифр: 1 2 3 4 5 6 7. Соедините их знаками плюс и минус так, чтобы получилось 40. (12+34-5+6-7=40.)

   2.За 4 часа 6 солдат начистили 4 ведра картошки. Сколько вёдер начистили бы 4 солдата за 3 часа?

3.Десяти собакам и кошкам скормили 56 галет. Каждой кошке досталось 5 галет, а каждой собаке — 6. Сколько было собак?

6.Итог занятия. Вопросы по теме занятия.

7. Рефлексия.

Что нового ты узнал на занятии?

Все ли тебе было понятно?

 У вас на столах лежат смайлики. Выбери тот, который соответствует твоему настроению.

« Занимательная математика»

Тема: Комбинаторика. Геометрия и счет. Логическая задача. «Спичечный» конструктор.

Цель: вызвать познавательный интерес к математике, умение найти правильный и оригинальный ответ в трудной ситуации, формирование умения работать в парах.

Задачи :

формирование умения рассуждать, как компонента логической грамотности;

освоение эвристических приемов рассуждений;

формирование интеллектуальных умений, связанных с выбором стратегии решения, анализом ситуации, сопоставлением данных;

развитие познавательной активности и самостоятельности учащихся;

формирование способностей наблюдать, сравнивать, обобщать, находить простейшие закономерности, использовать догадку, строить и проверять простейшие гипотезы;

формирование пространственных представлений и пространственного воображения;

привлечение учащихся к обмену информацией в ходе свободного общения на занятиях.

Работа над формированием УУД:

личностные:

— формирование положительного отношения к полученным знаниям

познавательные:

— формирование умения считать геометрические фигур в разбитой на части общей фигуры

коммуникативные:

— сотрудничество с учителем и сверстниками

— разрешение спорных ситуаций.

 Ожидаемые результаты:

Занятия в кружке должны помочь учащимся:

усвоить основные базовые знания по математике; её ключевые понятия;

помочь учащимся овладеть способами исследовательской деятельности;

формировать творческое мышление;

способствовать улучшению качества решения задач различного уровня сложности ;

формировать положительного отношения к полученным знаниям

формировать цели занятия

формировать умения классифицировать объект

сотрудничать с учителем и сверстниками,

разрешать спорные ситуации.

успешному выступлению на олимпиадах, играх, конкурсах.  

Оборудование:

1)тетрадь для работы в кружке

2) цветные карандаши

3) вспомогательные карточки для выполнения заданий.

4) чертежи на доске

Ход занятия

Прозвенел звонок,

Начинается кружок

Занимательный, увлекательный.

I. Разминка.

Крышка стола имеет 4 угла, один угол отпилили. Сколько углов осталось у стола? (5)

Горели 5 свечей, 2 из них погасли. Сколько свечей осталось?

1 термометр показывает 5 градусов мороза. Сколько градусов мороза покажут 2 термометра?

II. Сообщение темы занятия

Тема нашего занятия: комбинаторика, конструирование

III. Комбинаторика

Девочка Марина пошла к бабушке через лес. Перед ней три дороги. Сколькими способами может дойти Марина до бабушки?

— Чтобы вам легче было считать дорожки, у вас есть чертеж. Для того чтобы легче было считать можно использовать цветные карандаши, каждый путь обозначать разным цветом.

IV. Геометрия и счет.

На крыше дома Марина увидела вот такой рисунок.

Какое можно выполнить задание по этому рисунку?

  Приложение 1.

— Как сосчитать количество треугольников?

Маленькие треугольники(одноклеточные) побольше и

большие .

V. Логическая задача.

Проходя по дорожкам к бабушке Марина наблюдала как соревнуются сказочные герои. О чем рассказала бабушке. Послушайте ее рассказ.

Буратино, Незнайка, Чипполино и Карлсон соревновались в беге. и заняли 4места, причем никто из них не делил между собой место. Что это значит? Буратино — ни первое и ни третье. Чипполино — второе, Незнайка не был первым и последним. Какие места заняли сказочные герои?

— Как мы будем решать данную задачу?

+ С помощью таблицы, которая в тетради.

Первую клетку не занимаем. Слева пишем первой буквой имена тех кто соревнуется. Назовите их. В верху номера мест.

Я читаю еще раз, вы с помощью плюсов и минусов отмечаете что известно из задачи.

VI.» Спичечный» конструктор . Работа в паре.

Бабушка предложила Марине поиграть с палочками. Марина предлагает вам поиграть вместе с ней. Возьмите 15палочек. Выложите узор.

Приложение 2.

Переложите 2 палочки так, чтобы получилось 4квадрата.

VIII. Итог. Рефлексия.
Приложение к занятию кружка «Занимательная математика»
DOCX / 10.65 Кб

Занятие математического кружка (6-7 класс).

Тема: Теория графов

Цель: углубление и расширение знаний по математике; развитие математического кругозора, логического мышления; пробуждение и развитие устойчивого интереса учащихся к математике и ее приложениям; разностороннее развитие личности.

Оборудование: мультимедийный проектор (презентация «Теория графов»), карточки с домашним заданием, раздаточный материал.

Епиграф: «Спорьте, заблуждайтесь, ошибайтесь, но ради бога, размышляйте, и хотя криво, да сами». Г.Лессинг

Оргмомент

Ребята, сегодня мы проводим с вами очередное занятие математического кружка. И начинаем мы его с задачи

Дети шпионов перехватили шифровку:12342562756278. В ней разные цифры означают разные буквы, а одинаковые цифры -одинаковые буквы. У них получились варианты:

«думай и трудись»;

«привет от деда»;

«мой вопрос прост»;

«вперед к победам».

Какая расшифровка верна? ( Ответ:«мой вопрос прост»).

Давайте, вспомним условия, которые необходимо выполнять на занятии.

Первое условие-это быть точным; второе- быть ясным, и насколько можно простым.

Разминка.

(Вам предлагаются задачи на проверку внимания, задачи на смекалку ).

• Вы вошли в темную комнату. В коробке у вас всего одна спичка. В комнате находятся свеча, керосиновая лампа и готовая к растопке печь. Что Вы зажжете в первую очередь? (спичку ).

• Класс шел парами. Один из учеников посмотрел вперед и насчитал девять пар, затем обернулся и насчитал пять пар. Сколько всего учеников шло в колонне ? ( 30 учеников ).

• Дядька Черномор написал на листке бумаги число 20. Тридцать три богатыря передают листок друг другу, и каждый или прибавляет к числу или отнимает от него единицу. Может ли в результате получится число 10? ( Нет, не может. После того как листок побывает в руках у богатыря, число, на нем написанное, будет менять свою четность, т.е. станет четным, если было нечетное и наоборот. Это значит, что после 33-х изменений число станет нечетным, т.е. никак не сможет равняться 10).

• В коробке лежит 200 мячей одного размера, но разных цветов: зеленые, красные, синие и белые. В темноте берут несколько мячей. Какое наименьшее количество мячей нужно взять, чтобы среди них обязательно было 10 одного цвета? (Мы не знаем, сколько мячей каждого цвета в коробке, но цветов 4. Поэтому 9х4=36-неприемлимый результат. Нужно взять 36+1=37 мячей, чтобы среди них было 10 одного цвета).

• На гору ведут 5 дорог. Найти количество способов подняться и спуститься с него, если: а) Подниматься и спускаться одной и той же дорогой можно; б)подниматься и спускаться одной и той же дорогой нельзя.

(а) если подняться на гору дорогой 1, то спуститься с нее можно дорогами 1,2,3,4,5, то есть 5-тью способами. То же самое и для дорог 2,3,4,5. Всего существует 25 способов подняться и спуститься с горы; б) Если подниматься и спускаться одной и той же дорогой нельзя, то получим на 5 способов меньше. Тогда остается 20 способов).

Повторение. Решение задач.

1. В ковре размером 3х3 метра Коля проделал 8 дырок. Докажите, что из него можно вырезать коврик размером 1х1 м, не содержащий внутри себя дырок.

Решение:

Разрежем на 9 ковриков размером 1х1м. Ковриков-«клеток»-9, а дырок-«кроликов»-8. Т.к. 8

Учитель: В школьной программе нет этой темы, однако, на основе такого простого и даже чуть наивного принципа, математикам удается решать весьма трудные задачи, доказывать красивые теоремы, причем не только элементарные.

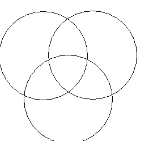
1. В одной семье было много детей. 7 из них любили капусту, 6 – морковь, 5 – горох, 4 – капусту и морковь, 3 – капусту и горох, 2 – морковь и горох, 1 – и капусту, и морковь, и горох. Сколько детей было в семье?

Решение:

Горох

1

Капуста

1

2

Горох

5

Капуста

7

3

1

1

3

1

2

4

Морковь

1

Морковь

6

Только капусту любит: 7-(2+3+1)= 1, только горох: 5-(2+1+1)=1, только морковь: 6-(3+1+1)=1.

Всего в семье 1+3+1+2+1+1+1=10 детей.

Ответ: 10 детей.

Учитель: Рисунки, которые нарисованы при решении этой задачи, называются «кругами Эйлера». Ученый писал, что «они очень подходят для того, чтобы облегчить наши размышления».

1. У меня зазвонил телефон,

— Кто говорит?

— Слон.

А потом позвонил крокодил…

А потом позвонили Зайчатки…

А потом позвонили Мартышки…

А потом позвонил Медведь…

А потом позвонили Цапли…

Итак, у Слона, Крокодила, Зайчаток, Мартышек, Медведя, Цапель и у меня установлены телефоны. Каждые два телефонных аппарата соединены проводом. Как сосчитать, сколько для этого понадобилось проводов?

Решение

Всего телефонных аппаратов 7, каждый соединен с шестью. Значит, соединений всего 7x6=42. А провод – это два соединения. Значит, всего понадобился 21 провод.

Ответ: 21 провод.

1. В одном дворе живут 4 друга. Вадим и шофер старше Сергея, Николай и слесарь занимаются боксом; электрик — младший из друзей. По вечерам Андрей и токарь играют в домино против Сергея и электрика. Определите профессию каждого из друзей.

Решение:

	Вадим	Сергей	Николай	Андрей
шофер	—	—	—	+
слесарь	—	+	—	—
электрик	—	—	+	—
токарь	+	—	—	—

Ответ: Андрей-шофер, Сергей-слесарь,Николай-электрик,Вадим-токарь.

Учитель: использование таблицы значительно ускоряет процесс решения.

1. Старатель намыл 8 мешочков золотого песка. Все они весят одинаково, кроме одного, который легче остальных, но на вид он совершенно такой же. Как старателю определить, какой мешочек легче других, всего за два взвешивания?

Решение: надо взять 6 мешочков и положить их по 3 на чашки весов. Этим взвешиванием старатель может определить, на какой чашке весов находится легкий мешочек. А если весы уравновесятся, значит, он среди тех двух мешочков, которые еще не взвешивали, и сравнивать их вес можно вторым взвешиванием. Если при первом взвешивании одна чашка оказалась легче, то надо из этих трех мешочков взять любые два и вторым взвешиванием сравнить их вес, а если весы уравновесятся, то это мешочек, который был отложен.

Проверка домашнего задания.

Слайд 1 (Задача не решается, и это тем досаднее, что она не решается только «чуть-чуть». Вторая же фигура легко вычерчивается одним непрерывным движением без повторений.

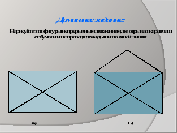
Почему так происходит? В этом нам сегодня и предстоит разобраться.

Введение в тему урока.

Вычерчивание фигур одним росчерком- тоже математическая задача! И относится она к теории графов (Слайд 2, Слайд 3)

Изучение новой темы.

Показ слайдов:4,5,6.

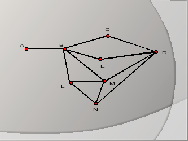
Слайд7: перед вами граф, назовите степень каждой вершины графа.

А теперь вернемся к домашнему заданию. Слайд 8

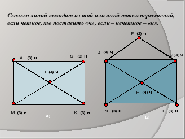
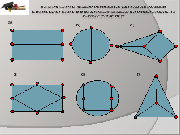
Давайте, попытаемся дать ответ на вопрос: в каком случае можно обрисовать фигуры не отрывая карандаш от бумаги и не проводя дважды по ни одной линии, а в каком случае нет?

Показ слайдов 9,10,11,12 ( граф, который можно нарисовать, не отрывая карандаша от бумаги, называется Эйлеровым)

Показ слайдов 13,14 ( Решение: ребра и вершины куба образуют граф, все 8 вершин которого имеют степень 3, и следовательно обход невозможен).

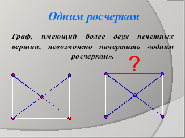
Решение задач.

1. Между 9 планетами Солнечной системы введено космическое сообщение. Ракеты летают по следующим маршрутам: Земля-Меркурий, Плутон-Венера, Земля-Плутон, Плутон-Меркурий, Меркурий-Венера, Уран-Нептун, Нептун-Сатурн, Сатурн-Юпитер, Юпитер-Марс и Марс-Уран. Можно ли добраться с Земли до Марса?

Нужно грамотно перевести это условие на язык теории графов.

Решение:

Нарисуем схему: планетами будут соответствовать точки, а соединяющими их маршрутами- непересекающиеся между собой линии. Теперь видно, что долететь от Земли до Марса нельзя.

Ме

З

Н

У

С

В

П

Ю

Ма

Ответ: долететь от Земли до Марса нельзя.

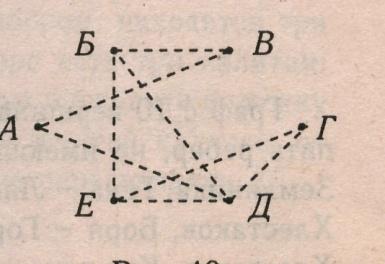
2.В первенстве класса по настольному теннису 6 участников: Андрей, Борис, Виктор, Галина, Дмитрий и Елена. Первенство проводится по круговой системе –каждый из участников играет с каждым из остальных один раз. К настоящему моменту некоторые игры уже проведены: Андрей сыграл с Борисом, Галиной и Еленой; Борис, как уже говорилось с Андреем и еще с Галиной; Виктор с Галиной, Дмитрием и Еленой; Галина – с Андреем и Борисом; Дмитрий – с Виктором и Елена- с Андреем и Виктором. Сколько игр проведено к настоящему моменту и сколько еще осталось?

Решение:

Изобразим данные задачи в виде графа. Участников будем изображать точками. Если двое участников уже играли между собой. То будем соединять изображающие их точки отрезками.

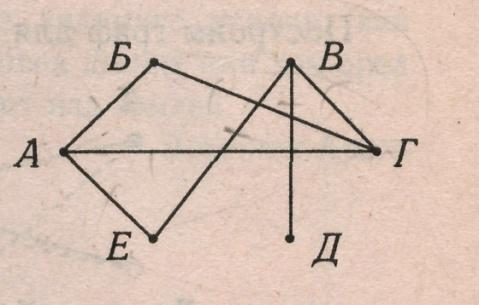
а) б)

Число проведенных игр 7 (рис. а). Нужно найти число игр, которые осталось провести. Для этого будем соединять тех участников, которые еще не играли друг с другом. Осталось провести 8 игр (рис. б).

Ответ: число проведенных игр 7, осталось провести еще 8 игр.

Слайд 15 (Разве нельзя прийти к решению чисто математическим путем.

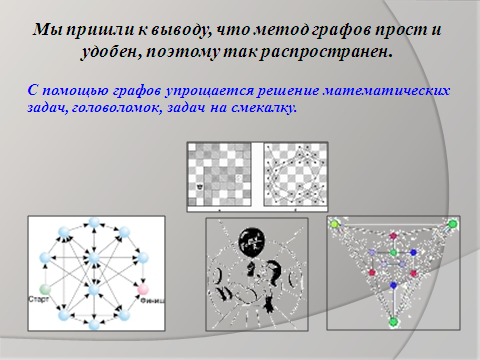
Да, можно. Но графы придали условию наглядность, упростили решение, а это не так уж мало).

Показ слайдов 17,18,19,20,21,22.

Сейчас почти в любой отрасли науки и технике встречаешься с графами (слайд 23):

• В электротехнике- при построении электрических схем;

• В химии и биологии- при изучении молекул и их цепочек;

• В географии- при составлении карт;

• В истории- при составлении генеалогических древ (родословной);

• В геометрии- чертежи многоугольников, многогранников, пространственных фигур;

• В экономике- при решении задач о выборе оптимального пути для потоков грузового транспорта.

О математике и говорить не приходится.

Домашнее задание — Слайд 24.

Итог урока – Слайд 25.

Наше занятие мне бы хотелось закончить словами венгерского математика Д.Пойа

«Решение задач- практическое искусство, подобное плаванию, катанию на лыжах или игре на фортепиано; научится этому можно, только беря пример с наилучших образцов и постоянно практикуясь. Но помните: если вы хотите научиться плавать, то смелее входите в воду, а если хотите научиться решать задачи, то решайте их».

ВВЕДЕНИЕ

Одним из приоритетных направлений современного российского образования является сохранение генофонда нации, обеспечение устойчивого динамического развития общества с высоким уровнем жизни. Обеспечение высоких показателей в данном направлении невозможно без создания в учебных заведениях необходимых условий для достижения нового, современного качества общего и профессионального образования.

В современных учебных заведениях при внедрении Федеральных государственных образовательных стандартов определенным образом должны соблюдаться рекомендации по применению методов не только в повышении уровня знаний, умений, навыков адаптации и социализации в обществе, но и в формировании культуры здоровья молодого поколения, так как умственное развитие обучающихся, их мировоззрение, прочность знаний и духовная жизнь зависит от бодрости и жизнедеятельности детей. Возросшая интенсификация образовательного процесса привела к увеличению учебной нагрузки. Поэтому, при обучении одним из ключевых направлений должна стать поддержка социального здоровья учащихся, помощь в преодолении стрессовых ситуаций, в целостной подготовке к оптимизации своей жизнеспособности.

В Концепции развития математического образования, утвержденной распоряжением правительства Российской Федерации от 24.12.2013 г. № 2506-р, отмечено: «Математика занимает особое место в науке, культуре и общественной жизни. Изучение математики играет главную роль в образовании, развивая познавательные способности человека». Поэтому очень важно заинтересовать учеников, чтобы они с увлечением занимались изучением математики. Один из подходов — популяризация математики через «присущую ей красоту и увлекательность».

Положение о проведении математического интеллектуального турнира «Формула успеха»

1. ЦЕЛИ И ЗАДАЧИ КОНКУРСА

Интеллектуальный турнир «Формула успеха» учрежден для студентов колледжа и направлен на развитие творческого потенциала преподавателей и студентов; поддержку новых технологий в организации образовательного процесса.

Цель турнира — популяризация математических знаний и математического образования, распространение педагогического опыта по формированию мотивации обучающихся.

Задачи турнира:

• формирование представлений о математике как универсальном языке науки, средстве моделирования явлений и процессов, необходимых в повседневной жизни, об идеях и методах математики;
• воспитание средствами математики культуры личности, отношения к математике как к части общечеловеческой культуры;
• формирование представления студентов об интеграции математики в другие предметы;
• понимания значимости математики для общественного процесса;
• развитие логики, пространственного мышления, мелкой моторики, усидчивости, памяти, смекалки, наблюдательности, внимательности, концентрации и достижение поставленной цели.

2. ОРГАНИЗАТОРЫ ТУРНИРА: Преподаватель математики — Богина Е.Ю.

3. УЧАСТНИКИ ТУРНИРА: студенты группы ТОД — 211, классный руководитель — Богина Е.Ю.

4. ПРОГРАММА ТУРНИРА И КРИТЕРИИ ОЦЕНКИ:

• Конкурс — «Разминка» — в течение 3-х минут преподаватель очень быстро задает вопросы. Один правильный ответ-1 балл. В конкурсе побеждает команда, давшая наибольшее количество правильных ответов.
• Конкурс — «Видеовопросы» — команды отвечают на вопросы, задаваемые студентами из видеороликов. На размышление — 1 минута. Правильный ответ оценивается в 1 балл.
• Конкурс — «Логическая дуэль» — ведущий задает командам логическую задачу — рассказывает часть запутанной истории. Команды по очереди задают вопросы ведущему чтобы распутать всю ситуацию. Ответ, наиболее близкий к правильному оценивается в 1 балл.
• Конкурс — «На лбу написано» — команды должны отгадать слова — математические термины. Условие: однокоренные слова употребляться не должны. На размышление — 2 минуты. Правильный ответ оценивается в 1 балл.
• Конкурс — «Битва титанов» — разгадывание механических головоломок — 3,4,5,6,7 баллов; конструирование — 2 балла за модель; решение задач по теории вероятностей — 5 баллов за задачу. Длительность конкурса — 10 минут.

Дополнительные баллы могут присуждаться команде за активное, участие дополнительные ответы — не более 5 баллов.

С команды могут быть сняты баллы за недостойное поведение членов команды, болельщиков этой команды во время турнира (на усмотрение жюри).

5. ВРЕМЯ И МЕСТО ПРОВЕДЕНИЯ: в 14.45, актовый зал 4 корпуса.

6. СОСТАВ ЖЮРИ:

• Председатель: — зав. отделом информационных технологий — Коновалов В. Н.;
• Зав. отделением «Транспорта и сервиса на транспорте» — Извозчикова И.А.
• Преподаватель информатики — Каклюгина И.Д.

7. НАГРАЖДЕНИЕ: Победители награждаются грамотами и призами.

Сценарий математического интеллектуального турнира

«ФОРМУЛА УСПЕХА»

Добрый день, дорогие друзья и любители математики!

Мы рады вас приветствовать на математическом интеллектуальном турнире «Формула успеха», приуроченном к празднику «День России».

Уважаемые студенты, вы — молодое, подрастающее поколение, являетесь надеждой, будущим нашей страны. А математика занимает особое место в науке, культуре и общественной жизни. Изучение математики играет главную роль в образовании, развивая познавательные способности человека». Один из подходов в этом развитии — популяризация математики через «присущую ей красоту и увлекательность».

В качестве эпиграфа нашего сегодняшнего мероприятия я выбрала слова Великого французского математика Б.Паскаля: «Предмет математики настолько серьезен, что полезно не упускать случаев делать его немного занимательным».

И действительно, математика нужна всем людям на земле. Без математики человек не сможет решать, мерить и считать. Невозможно построить дом, сосчитать деньги в кармане, измерить расстояние. Если бы человек не знал математику, он не смог бы изобрести самолет, автомобиль, телевизор, холодильник и любую другую технику или программу. Математика нужна в истории, физике, инженерной графике. Математика позволяет человеку думать.

«Никакой достоверности нет в науках там, где нельзя приложить ни одной из математических наук, и в том, что не имеет связи с математикой».

Так сказал Леонардо да Винчи — итальянский художник, скульптор и ученый, анатом, естествоиспытатель.

В нашем турнире сегодня принимают участие 2 команды: «Люди икс» и «Люди игрек».

Члены жюри:

• Председатель: — зав. отделом информационных технологий — Коновалов В. Н.;
• Зав. отделением «Транспорта и сервиса на транспорте» — Извозчикова И.А.;
• Преподаватель информатики: Каклюгина И.Д.

Первый конкурс называется «Разминка»

Я буду задавать вопросы, команды будут отвечать на скорость. За каждый правильный ответ команда получит 1 фишку в виде геометрической фигурки. Мы попросим жюри вести учет. Начинаем.

Задачи для разминки

1. Сколько раз можно вычесть 3 из 25? (1, т.к. второй раз вы уже будете вычитать из 22).
2. Двое играли в шахматы 2 часа. Сколько времени играл каждый? (2 часа).
3. Какой знак надо поставить между двумя двойками, чтобы получилось число больше 2 и меньше 3? (запятую).
4. Что больше произведение или сумма десяти цифр от 0 до 9? (произведение равно 0. Сумма больше).
5. На руках 10 пальцев. Сколько пальцев на 10 руках? (50).
6. Зайцы распилили бревно. Они сделали 10 распилов. Сколько получилось чурбачков? (11).
7. Шла старуха в Москву. Навстречу ей три старика. У каждого старика по мешку, в каждом мешке по коту. Сколько существ направлялось в Москву? (одна старуха).
8. Если красную тряпку окунуть в черное море какой она станет? (мокрой).
9. Если работа не волк, то что тогда? (произведение силы на расстояние).
10. Представьте, что ваш дом имеет 4 стены и каждая из этих стен имеет вид на юг. Рядом с вашим домом гуляет медведь. Вопрос: какого цвета медведь? (белый. Вы на северном полюсе).
11. Электропоезд движется на север со скоростью 100 км/ч. Ветер дует с запада со скоростью 10 км/ч. В какую сторону движется дым от поезда? (У электропоезда нет дыма).
12. Какой рукой лучше всего размешивать кофе со сливками и с сахаром? (той, в которой ложка).
13. Почему птицы летят на юг? (потому, что пешком идти долго).
14. Как засунуть жирафа в холодильник? (взять жирафа, открыть дверь, засунуть жирафа, закрыть дверь).
15. Как засунуть слона в холодильник? (Открыть дверь, вытащить жирафа, засунуть слона, закрыть дверь).
16. Лев созвал всех зверей на собрание. Явились все, кроме одного. Что это за зверь? (Слон, ведь он в холодильнике).
17. Вам нужно переплыть широкую реку, которая кишит крокодилами. Как это можно сделать? (Надо срочно переплыть реку пока все крокодилы на собрании).
18. Почему студенты опаздывают на занятия? (Потому, что учиться никогда не поздно).
19. Что лучше всего повышает квалификацию водителя? (едущая за ним, машина ГИБДД).
20. Если студент будет плохо учиться, то что произойдет, то что произойдет? (Праздник 23 февраля станет для него профессиональным).

— Итак, первый конкурс завершен, жюри подводит итоги.

Второй конкурс «Видеовопросы»

С экрана вам будут задавать вопросы, ваша задача ответить правильно. Команда, первая давшая правильный ответ, получит 1 балл.

1 вопрос: В Новочеркасске, на соборной площади стоит Вознесенский Кафедральный собор. Подскажите, как без лестницы измерить высоту собора?

Ответ: Самый легкий и самый древний способ, тот, которым греческий мудрец, философ и математик Фалес Милетский за шесть веков до нашей эры определил в Египте высоту пирамиды. Он воспользовался ее тенью. Жрецы и фараон, собравшиеся у подножия высочайшей пирамиды, озадаченно смотрели на северного пришельца, отгадывавшего по тени высоту огромного сооружения. Фалес, — говорит предание, — избрал день и час, когда длина собственной его тени равнялась его росту; в этот момент высота пирамиды должна также равняться длине отбрасываемой ею тени.

Я заметил, что в 10.30 утра длина моей тени равна моему росту, а значит в это же время длина тени собора равна его высоте.

2 вопрос: 5 стоит 2 рубля, 54 стоит 4 рубля. Что я покупаю и сколько стоит 504?

Ответ: Покупали номера для квартиры. 504 стоит 6 рублей.

3 вопрос: Отгадайте ребус. (Задача)

— Просим жюри объявить результат за два конкурса.

Третий конкурс «Логическая дуэль»

Я вам буду задавать логическую загадку, т.е. описывать часть запутанной истории, а вы должны восстановить всю ситуацию. Вы можете задавать мне вопросы, но только такие, на которые я могу ответить только «да», «нет» или «несущественно».

Ситуация первая: Бежит мужик с ружьем, а за ним толпа. Он останавливается, стреляет 5 раз, кричит: «Не видать вам моего золота!» и бежит дальше.

— Что это за ситуация? Задавайте вопросы.

Ответ: Биатлон.

Ситуация вторая: В детской больнице юные пациенты очень любили играть с очаровательными плюшевыми мишками, которые были там. К сожалению, дети любили их так сильно, что мишки исчезали с пугающей скоростью: малолетние пациенты уносили их с собой. Как руководство больницы решило эту проблему?

Ответ: Всем мишкам сделали повязки и сказали маленьким детям, что мишкам надо оставаться в больнице чтобы вылечиться. Дети с грустью, но с сочувствием согласились.

Ситуация третья: У человека была книга стоимостью 40 000 долларов. Однако он сознательно уничтожил ее. Почему?

Ответ: Человек имел два экземпляра этой книги. И один экземпляр уничтожил, чтобы повысить стоимость второго.

— Просим жюри подвести итоги за 3 конкурса.

Четвертый конкурс: «НА ЛБУ НАПИСАНО»

Надо угадать как можно больше математических терминов. Условие: однокоренные слова употребляться не должны. (в течение 2 минут команды формулируют правильные ответы, каждый правильный ответ — 1 балл). Побеждает команда, отгадавшая больше терминов. От каждой команды нужны 5 участников.

— Начинаем. От каждой команды вызывается по 5 человек, им предлагается отгадать 5 математических терминов: (на примере слова — биссектриса).

• 1 команда: пирамида, апофема, конус, сфера, грань;
• 2 команда: куб, ребро, цилиндр, шар, диагональ.

— Прошу жюри подвести итоги 4 конкурса.

Конкурс: «Битва титанов»

В этом конкурсе надо продемонстрировать умение разгадывать головоломки, конструировать и решать задачи по теории вероятностей.

— Выберите по 8 человек от каждой команды. Великие головоломщики и конструкторы, должны занять места за столом, а великие вычислители вероятностей должны выйти к доске.

(ведущий раздает головоломки, конструкторы и задания).

— Для разгадывания предлагаются головоломки:

• «Красный круг» — уровень сложности 7 баллов из 7-ми. Задание: все шесть элементов необходимо уложить в квадратную рамку.
• «Теремок» — уровень сложности 4 балла из 7-ми. Задание: собрать тело кубической формы из шести составных элементов.
• «Упаковка» — уровень сложности 5 баллов из 7-ми. Задание: из девяти кубиков собрать предложенную фигуру.
• «Упрямоугольник» — уровень сложности 6 баллов из 7-ми. Задание: из четырех частей собрать прямоугольник.
• «Звезда» — уровень сложности 3 балла из 7-ми. Из шести элементов собрать невыпуклый многогранник.

— С помощью конструктора предлагается собрать модели многогранников и тел вращения:

• 1 команда: правильная шестиугольная призма, шаровой сегмент.
• 2 команда: правильная четырехугольная пирамида, шаровой сектор.

— Решить задачи по теории вероятностей.

1 команда: Ковбой Джон попадает в муху на стене с вероятностью 0,9, если стреляет из пристрелянного револьвера. Если Джон стреляет из непристрелянного револьвера, то он попадает в муху с вероятностью 0,2. На столе лежит 10 револьверов, из них только 4 пристрелянные. Ковбой Джон видит на стене муху, наудачу хватает первый попавшийся револьвер и стреляет в муху. Найдите вероятность того, что Джон промахнётся. (0,52).

2 команда: В магазине стоят два платёжных автомата. Каждый из них может быть неисправен с вероятностью 0,05 независимо от другого автомата. Найдите вероятность того, что хотя бы один автомат исправен.

Жюри засекает время 10 минут. (0,9975).

— Итак, время вышло. Подводим итоги последнего конкурса и итоги всего турнира.

— Поздравляем победителей (команды жмут друг другу руки, звучат фанфары).

— Приз победителям — плюс один балл на экзамене.

— А главное, сегодня мы вывели «Формулу успеха»

УСПЕХ = 1% ТАЛАНТА + 99% ТРУДА

— На этом, наш турнир завершен. Спасибо за внимание!

ФОТООТЧЕТ

Использованная литература

1. Перельман Я.И. Живая математика: Математические рассказы и головоломки: 9-е изд. — М.: 2010.
2. Перельман Я.И. Веселые задачи: 101 головоломка для юных математиков. — Пг.: 1916.
3. Красноухов В.И. Головоломки [Electronic resource] URL: http://www.planetagolovolomok.ru/articles (Дата обращения 20.08.2018).
4. Красноухов В.И. Занимательный мир механических головоломок [Electronic resource] URL: http://www.terrakid.ru/nash-blog/informatsiya-k-ra… (Дата обращения 19.08.2018).

Занятие математического кружка по теме «Тайны квадрата»

Данный урок проводится в нестандартной форме. Нестандартные способы обучения способствуют поддержанию интереса к предмету, развитию чувства ответственности каждого ученика за конечный результат, дают возможность проявить каждому ученику свои способности. Учащиеся на подобных уроках получают хороший эмоциональный заряд, так как урок проходит в непринужденной доброжелательной обстановке. Сопровождение урока презентацией повысить заинтересованность обучающихся, поддерживать интерес к предмету, быстро включить класс в деловой ритм, организовать внимание всех обучающихся.

Цели: повышение мотивации учащихся к обучению.

Задачи:

Образовательная: расширить представление учащихся о квадрате;

Развивающая: развитие зрительной памяти, математически грамотной речи, логического мышления, развитие навыков работы с дополнительной литературой, с историческим материалом;

Воспитывающая: воспитание познавательной активности, культуры общения, культуры диалога, воспитание эстетических качеств и умения общаться.

Формы работы на уроке: групповая работа

Ход

Добрый день, дорогие ребята!

Я сегодня вас приглашаю в “Мастерскую конструирования знаний» и даю вам напутственные слова.

Мир полон тайн –
Постигни их.
Решения смелые прими –
К открытиям прекрасным
Придешь путем отважным.

Я предлагаю вам назвать тему нашей мастерской, но для этого нужно ответить на вопрос: (слайд)

О какой геометрической фигуре идёт речь?

Геометрическая фигура, имеющая ряд мифологических, символических и иных нетрадиционных толкований. Какие есть варианты? Среди вариантов есть правильный ответ, но давайте прочитаем дальше.

Наиболее явно связана с числом четыре, символизирующим такие понятия, как порядок, равенство, истина, справедливость, мудрость, честь, искренность, земля.

Символизирует четыре стороны света, четыре времени года, четыре человеческих возраста, четыре основные элемента мира (огонь, вода, земля, воздух)

Итак, тема мастерской: «Тайны квадрата».

Цель: выяснить насколько интересна эта фигура, как много может сделать человек, владеющий информацией о квадрате.

А теперь давайте выясним, где в нашей жизни, не считая школьной геометрии, можно встретить квадрат?

Индивидуальная практическая работа.

Перед каждым из Вас квадрат, разрезанный на 7 геометрических фигур. Будем называть их так: два больших равных треугольника, два маленьких равных треугольника, один средний треугольник, один квадрат, один параллелограмм.

Задание заключается в том, чтобы каждому собрать из имеющихся фигур квадрат.

Какие ассоциации вызывает у вас получившийся квадрат?

Ну, конечно, Чёрный квадрат Каземира Малевича.

(слайд )

Так, значит, квадрат можно встретить в живописи.

Занимательных задач на разрезание – множество. Многие из них имеют древнее историческое происхождение. Одна из самых известных древних геометрических головоломок – игра «танграм», в которую в течение многих веков играют и дети, и взрослые. Возникла игра в Китае, где она называется «чи чао ту», то есть умственная головоломка из семи частей.

А теперь поработаем в группах.

Следующая задача заключается в самостоятельном составлении своих фигур из частей танграма по тем же правилам.

Головоломка состоит в том, что нужно используя все семь частей, сложить фигурки, предложенные на рисунке Фигуры должны примыкать друг к другу, не накладываясь при этом друг на друга.

1 группа	2 группа	3 группа
подсказка	подсказка	подсказка

Таких фигур можно составить очень много, вот, например, ещё несколько

(слайд «Танграмм»)

Далее ученики представляют домашнее задание. Класс был разделен на 3 группы:

исследователи «Квадрат через призму урока математики»

практики«Квадрат через призму урока технологиии»

пользователисети Интернет «Квадрат через призму урока информатики»»

Защита своих проектов, итогов исследования (Выступают из каждой группы по 1 ученику).

1) Квадрат замечателен уже тем, что, в отличие от других геометрических фигур, он имеет несколько определений.

2) Оригами из квадрата. Сделаем тюльпан.

3) Магический квадрат. Квадрат Пифагора.

Пифагор был мистиком. он Считал, что с помощью его квадрата можно предсказать характер и судьбу человека по его дате рождения.

Вы поделились своими находками, каждый открыл для себя что-то новое.

(слайд «Лоскутное шитьё»)

Конечно же, мы посмотрели лишь малую часть того, что можно знать и сделать из такой удивительной геометрической фигуры как квадрат.

Итог:

Мы пришли к выводу, что квадрат действительно удивительная геометрическая фигу­ра, имеет много замечательных, интересных свойств.

Квадрат до сегодняшних дней привлекает к себе внимание. Знания о квадрате имеют огромное значение для применения на практике, к его свойствам обращаются и дизайнеры, и архитекторы, и военные стратеги, и многие другие.

Я думаю, Вы согласитесь со мной: на уроке, как и в жизни всегда должно быть место творчеству. Именно этим мы сегодня и занимались.

Каждый из вас почувствовал себя творцом!

Слышим часто мы слова – математика трудна!

Да, трудна, но интересна — в жизни ей всегда есть место.

Посмотрите-ка, друзья,– без неё прожить нельзя.

Здесь – квадрат, а вот вам – круг, Математика вокруг!

Человеческая мысль не стоит на месте. А потому в настоящее время существует танграммы, решённые на базе круга, который является не менее загадочной геометрической фигурой.

Включив пространственное воображение, из полученных частей фигуры составьте дома силуэты разных зверюшек, птичек и человечков.

Главное соблюдать правило: для составления силуэта надо использовать все 10 частей, не накладывая одну на другую.

Спасибо вам, за то, что вы работали со мной в мастерской конструирования знаний.

Примите в благодарность от меня тюльпан, сделанный из удивительного квадрата, но нам его не во что поставить, давайте быстренько сделаем для него стаканчик.

Желаю всем шумных успехов и буйного разгула фантазии!

1.    
Образовательные:

• выявить, обобщить и расширить математические знания, имеющиеся у детей на данный момент в области решения логических задач;
• ввести понятие «граф»;
• начать формирование умений по применению знаний в решении заданий;

2.    
Развивающие:

• развивать логическое мышление, долговременную память, внимательность;
• развивать умение рассуждать, обобщать и делать выводы;
• развивать правильную математическую речь, вычислительный навык;

3.    
Воспитательные:

• воспитывать усидчивость, дисциплинированность, инициативность;
• воспитывать уважение к преподавателю, одноклассникам.

рыжие

черные

русые

Белов

+

—

—

Чернов

—

—

+

Рыжов

—

+

—

4.    
^ Практический этап

Разработка занятия кружка по теме «Задачи, решаемые с помощью графов»Цель: Ввести новые знания по теме «Задачи, решаемые с помощью графов»Задачи:

Образовательные:выявить, обобщить и расширить математические знания, имеющиеся у детей на данный момент в области решения логических задач;ввести понятие «граф»;начать формирование умений по применению знаний в решении заданий;Развивающие:развивать логическое мышление, долговременную память, внимательность;развивать умение рассуждать, обобщать и делать выводы;развивать правильную математическую речь, вычислительный навык;Воспитательные:воспитывать усидчивость, дисциплинированность, инициативность;воспитывать уважение к преподавателю, одноклассникам.Ход мероприятия1. Организационный момент: Здравствуйте, садитесь! Сегодня на занятии вы познакомитесь с новым видом задач.2. Подготовительный этап.А) «Мозговая гимнастика»^ Качания головой: дышите глубоко, расслабьте плечи и уроните голову вперед. Позвольте голове медленно качаться из стороны в сторону, пока при помощи дыхания уходит напряжение. Подбородок вычерчивает слегка изогнутую линию на груди по мере расслабления шеи. Выполнять 30 секунд.«Ленивые восьмерки»: нарисуйте в воздухе в горизонтальной плоскости « восьмерки» по три раза каждой рукой, а затем обеими руками.« Зоркие глазки»: глазами нарисуйте 6 кругов по часовой стрелке и 6 кругов против часовой стрелки.^ Б) Разминка- Что можно подержать только в левой руке? ( свой правый локоть).- Какие две ноты растут в огороде? (Фа-соль)- Во время грозы мы наблюдаем молнию и гром. А что вы слышите между ними? ( Союз и)- У Егора было 10 овец. Всех, кроме 9 съел волк. Сколько овец осталось? (9)Вы уже знакомы с некоторыми логическими задачами, решаемыми с помощью таблиц и схем. Я вам предлагаю решить следующую задачу: Беседуют трое друзей: Белов, Рыжов, и Чернов. Брюнет сказал Белову: «Любопытно, что один из нас блондин, другой брюнет, третий — рыжий , но ни у кого цвет волос не соответствует фамилии» Какой цвет волос у каждого из друзей?- Что необходимо нам составить для решения подобной задачи? (таблицу)- Что запишем по горизонтали? ( фамилии)- Что будет по вертикали? ( цвет волос)- Сколько столбцов, а сколько строк? ( 3 на 3)

рыжие

черные

русые

Белов

Чернов

Рыжов

По условию задачи таблица заполняется .^ 3.Введение новых знанийИногда решение нестандартной задачи целесообразно оформить в виде графа. В ходе решения задачи вычерчивается граф- фигура, состоящая из отдельных вершин, соединенных друг с другом. Главные данные изображаются точками, а соответствия между ними сплошной линией, а если они не вязаны друг с другом – пунктиром. Точки называются вершинами графа, а линии — его ребрами.Фактически люди часто пользуются графами, не догадываясь об этом. Ведь те рисунки, на которых объекты изображены в виде точек, кружков, квадратиков, а связи между ними в виде линий, не что иное, как графическое изображение объекта.Предлагается следующая задача:Несколько мальчиков встретились на вокзале, чтобы поехать за город в лес. При встрече все они поздоровались друг другом за руку. Сколько мальчиков поехало за город, если всего было 10 рукопожатий? — Как вы думаете, сколько могло быть мальчиков? (3, 4, и т.д) — Каким способом вы пытались посчитать? (подбором, можно провести эксперимент , посчитать на практике ). — Получилось ли у вас решить задачу быстро? ( нет) — Всегда ли можно воспользоваться этими способами решения ? ( нет, могут быть слишком большие числа, не хватает людей для практического эксперимента). Предлагаю вам новый способ решения задачи, который затратит у вас меньше времени.Решение. Предположим, что встретились два мальчика, изобразим их точками, а рукопожатие линией, соединяющей эти точки (рис. а). Добавляем третьего приятеля и получаем три рукопожатия (рис. 6). Значит, необходимо добавить еще четвертого мальчика. Если встретились четыре мальчика, то рукопожатий будет шесть (рис. в). Необходимо добавить следующего, пятого мальчика. На получившемся графе видно, что рукопожатий получилось 10 (рис. г). Следовательно, на вокзале встретились пять мальчиков. — Считаете ли вы этот способ оптимальным, удобным? (да)

^ Практический этап- Ребята, предлагаю вам решить следующую задачу « Меню»В школьной столовой на первое можно заказать щи, гороховый суп и борщ, на второе – котлету и рыбу, а на третье — чай и морс. Сколько вариантов обеда можно получить из указанных блюд? -Закончите составление дерева и покажите цветным карандашом путь, который соответствует обеду « гороховый суп, котлета, морс»морс чайрыба котлетаБорщ г.суп щи — Один ученик выполняет на доске, а остальные в тетради. Ответ: 12 вариантов- Предлагаю решить самостоятельно следующую задачу.2. В стране Алфавит 8 городов: А, Б, В, Г, Д, Е, Ж. 3и 8 непересекающихся дорог между городами А и Б, Е и Д, Б и Ж , З и А,В и Г, Г и Д, Ж и З, В и Е.. Можно ли по этим дорогам из А в Г? При затруднение помочь начертить граф.Решение. Построим по условию задачи граф, при этом все вершины графа сразу отмечать не будем. Начнем с построения ребер графа, учитывая то условие, что они не пересекаются. Построим отрезки АБ и ЕД, присоединим к отрезку АБ отрезки БЖ и ЗА. Построим отрезок ВГ, не пересекающий ни один из построенных отрезков, и соединим точки Г и Д, Ж и З, В и Е (не обязательно отрезками, можно и кривыми линиями). По графу видно, что точки А и Г друг с другом не соединены, а значит по указанным дорогам из города А в город Г проехать нельзя.5. Игры со спичками1. Длина каждой палочки б см. Как из 13 таких палочек сложить метр? Ответ: Сложить из палочек слово метр. 2. Как сделать из двух спичек десять, не ломая их? Ответ: спички надо сложить в виде римской цифры «десять» : Х. 3.Как сделать из трех спичек шесть, не ломая их? Ответ: VI4.Как сделать из четырех спичек семь, не ломая их? Ответ: VII.